ত্ৰিভূজ | Triangle | Lesson 6 | Exercise 6.3 | Class 10 Mathematics Solution Assamese Medium | Class 10 Maths Solution Assam | দশম শ্ৰেণীৰ গণিতৰ প্ৰশ্ন উত্তৰ |

পাঠ ৬

ত্ৰিভূজ

Triangle

Exercise 6.3

1. চিত্ৰত দিয়া ত্ৰিভূজবিলাকৰ কোনবিলাক যোৰ সদৃশ উল্লেখ কৰা। উত্তৰটো দিয়াৰ ক্ষেত্ৰত কি সাদৃশ্য চৰ্ত ব্যৱহাৰ কৰিলা লিখা আৰু সদৃশ হোৱা ত্ৰিভূজবিলাক প্ৰতীকেৰে প্ৰকাশ কৰা।

(i)

∆ABC 〜 ∆PQR (AAA)

(ii)

∆ABC 〜 ∆PQR (SSS)

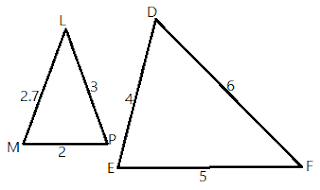
(iii) 

∆ LMP ≁ ∆ DEF

(iv) 

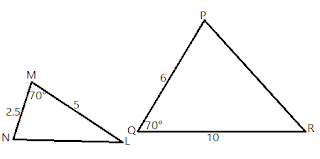
∆ LMN ≁ ∆ PQR

(v) 

∆ ABC ≁ ∆ DEF

(vi) 

∆ DEF ≁ ∆ PQR

2. চিত্ৰত ∆ ODC 〜 ∆ OBA, ∠BOC = 125॰ আৰু ∠CDO = 70॰। ∠DOC, ∠DCO আৰু ∠OAB নিৰ্ণয় কৰা।

উত্তৰঃ 

দিয়া আছে;

∠BOC = 125॰

∴∠DOC = 55॰ (∵∠DOC + ∠BOC = 180॰)

আৰু ∠CDO = 70॰

আকৌ,  ∠DCO + ∠COD + ∠CDO = 180॰

⇒∠DCO + 55॰ + 70॰ = 180॰

⇒∠DCO = 180॰ - 125॰

⇒∠DCO = 55॰

আকৌ, 

∆COD 〜∆AOB

∴ ∠ DCO = ∠OAB = 55॰

8. ABCD সামন্তৰিকৰ AD বাহুৰ বৰ্ধিত অংশত E এটা বিন্দু আৰু BE ৰেখাই CD ক F বিন্দুত ছেদ কৰে। দেখুওৱা যে ∆ABE 〜 ∆CFB। 

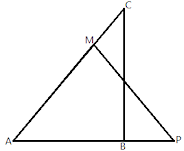
9. চিত্ৰত ABC আৰু AMP দুটা সমকোণী ত্ৰিভূজ। ইহঁতৰ সমকোণ দুটা ক্ৰমে B আৰু M। প্ৰমাণ কৰা যে 一 

10. ∆ABC আৰু ∠EFG ৰ AB আৰু FE বাহুত ক্ৰমে D আৰু H দুটা বিন্দু। CD আৰু GH ক্ৰমে ∠ACB আৰু ∠EGH ৰ সমদ্বিখণ্ডক।

যদি ∆ABC 〜 ∆FEG, দেখুওৱা যে 

11. চিত্ৰত ABC সমদ্বিবাহু ত্ৰিভূজৰ AB = AC আৰু CB ৰ বৰ্ধিত অংশত E এটা বিন্দু। যদি AD⊥AC, তেন্তে প্ৰমাণ কৰা যে ∆ABD〜∆ECF.

12. ABC ত্ৰিভূজৰ দুটা বাহু AB আৰু BC আৰু মধ্যমা AD ৰ লগত PQR ত্ৰিভূজৰ ক্ৰমে দুটা বাহু PQ আৰু QR আৰু মধ্যমা PM সমানুপাতিক। দেখুওৱা যে ∆ABC 〜∆PQR.

13. ABC ত্ৰিভূজৰ BC বাহুৰ ওপৰত D এটা বিন্দু আৰু ∠ADC = ∠BAC. দেখুওৱা যে CA² = CB.CD.

14. ত্ৰিভূজ ABC ৰ দুটা বাহু AB আৰু AC ৰ মধ্যমা AD আন এটা ত্ৰিভূজ PQR ৰ ক্ৰমে দুটা বাহু বাহু PQ আৰু PR আৰু মধ্যমা PM ৰ লগত সমানুপাতিক। দেখুওৱা যে ∆ABC ~ ∆PQR.

উত্তৰঃ 

15. 6m ওখ এটা উলম্ব খুটাঁৰ ভূমিত হোৱা ছাঁৰ দীঘ 4m আৰু একে সময়তে এটা টাৱাৰৰ ছাঁৰ দীঘ 28m। টাৱাৰটোৰ উচ্চতা নিৰ্ণয় কৰা।

উত্তৰঃ 

∴ টাৱাৰটোৰ উচ্চতা = 42 m

16. ABC আৰু PQR ত্ৰিভূজ দুটাৰ মধ্যমা ক্ৰমে AD আৰু PM। যদি ∆ABC 〜∆PQR, তেন্তে প্ৰমাণ কৰা যে AB/PQ = AD/PM।

উত্তৰঃ 

- Hiru Moni Bora

Post Id: DABP001110