Andhra Pradesh AP Board Class 9 Physics Chapter 4 Solution (Telugu Medium)| ఆంధ్రప్రదేశ్ బి.ఎ.ఎ.పి. బోర్డు 9 వ తరగతి భౌతికశాస్త్రం అధ్యాయం 4 పరిష్కారం (తెలుగు మీడియం)|

 Chapter 4

ప్రశ్న 1.ఎలక్ట్రాన్ ఆవేశం, ద్రవ్యరాశి ఎంత ఉంటాయి? ఎలక్ట్రాన్ ఆవేశానికి, ద్రవ్యరాశికి గల నిష్పత్తి ఎంత?

జవాబు:

ప్రశ్న 2.ఒక మోల్ ఎలక్ట్రాన్ల ఆవేశాన్ని గణించండి.

జవాబు:ఒక ఎలక్ట్రాన్ యొక్క ఆవేశం ఒక మోల్ ఎలక్ట్రాన్ల ఆవేశం
= – 1.602 × 10-19 coloumbs
= 6.023 × 1023 × 1.602 × 10-19
= 96488.5 coloumbs

ప్రశ్న 3.ఒక మోల్ ఎలక్ట్రాన్ల ద్రవ్యరాశిని గణించండి.

జవాబు:ఎలక్ట్రాన్ ద్రవ్యరాశి = 9.1 × 10-31 kg
ఒక మోల్ ఎలక్ట్రాన్ల ద్రవ్యరాశి = 6.023 × 1023 × 9.1 × 10-31
= 5.48 × 10-7 kg.

ప్రశ్న 4.ఒక మోల్ ప్రోటాన్ల ద్రవ్యరాశిని గణించండి.

జవాబు:ప్రోటాన్ ద్రవ్యరాశి = 1.672 × 10-27 kg
ఒక మోల్ ప్రోటాన్ల ద్రవ్యరాశి = 6.023 × 1023 x 1.672 × 10-27
= 1.00704 × 10-3 kg.

ప్రశ్న 5.ఒక మోల్ న్యూట్రాన్ల ద్రవ్యరాశిని గణించండి.

జవాబు:న్యూట్రాన్ ద్రవ్యరాశి 1.675 × 10-27 kg
ఒక మోల్ న్యూట్రాన్ల ద్రవ్యరాశి
= 6.023 × 1023 × 1.675 × 10-27
= 1.0088 × 10-3 kg.

ప్రశ్న 6.6C13, 8O16 12Mg24, 26Fe56, 38Sr88 కేంద్రకాలలో ఉండే న్యూట్రాన్ల, ఎలక్ట్రాన్ల సంఖ్య ఎంత
జవాబు:

(zxA)	ఎలక్ట్రాన్ల సంఖ్య (Z)	న్యూట్రాన్ల సంఖ్య (A – Z)
i) 6 C13	6	13 – 6 = 7
ii) 8O16	8	16 – 8 = -8
iii) 12Mg14	12	24 – 12 = 12
iv) 26 Fe56	26	56 – 26 = 30
v) 38Sr88	38	88 – 38 = 50

ప్రశ్న 7.కృష్ణ పదార్థం అంటే ఏమిటి?

జవాబు:ఏ పదార్థం తానిపై పడే వికిరణాలను ఎటువంటి ప్రతిబింబం లేకుండా పూర్తిగా గ్రహించగలుగుతుందో దానిని కృష్ణ పదార్థం లేదా నల్ల పదార్థం అని అంటారు. ఈ పదార్థం శోషించుకున్న మొత్తం శక్తిని అవసరమైతే తిరిగి వికిరణ రూపంలో విడుదల చేసే లక్షణం కలిగి ఉంటుంది.

ప్రశ్న 8.బామర్ శ్రేణి విద్యుదయస్కాంత వర్ణపటంలో ఏ ప్రాంతానికి చెందింది?
జవాబు:హైడ్రోజన్ పరమాణువులో ఎలక్ట్రాన్‌ ఎత్తైన శక్తి స్థాయిలు (n = 3, 4, 5 …) నుండి రెండవ శక్తి స్థాయి (n = 2) లోకి మారినప్పుడు వెలువడే వికిరణ గీతలను బామర్ శ్రేణి అంటారు. ఈ గీతలు విద్యుదయస్కాంత వర్ణపటంలో దృశ్య కాంతి ప్రాంతానికి చెందినవిగా కనిపిస్తాయి.

ప్రశ్న 9.పరమాణు ఆర్బిటాల్ అంటే ఏమిటి?
జవాబు:పరమాణువులో కేంద్రకం చుట్టూ ఉన్న త్రిమితీయ స్థలంలో ఒక ఎలక్ట్రాన్‌ కనుగొనే అవకాశం అత్యధికంగా ఉండే ప్రదేశాన్ని పరమాణు ఆర్బిటాల్ అని నిర్వచిస్తారు. అంటే, Ψ² విలువ గరిష్ఠంగా ఉండే స్థలమే ఎలక్ట్రాన్ పరమాణు ఆర్బిటాల్ అవుతుంది.

ప్రశ్న 10.హైడ్రోజన్ పరమాణువులో ఎలక్ట్రాన్ n = 4 కక్ష్య నుంచి n = 5 కక్ష్యకు మార్పు చెందినప్పుడు గ్రహించిన కాంతిరేఖ వర్ణపట శ్రేణిలో దేనికి చెందుతుంది?

జవాబు:హైడ్రోజన్ పరమాణువులో ఎలక్ట్రాన్ ఐదవ శక్తి స్థాయి (n = 5) నుండి నాలుగవ శక్తి స్థాయి (n = 4) కి మారినప్పుడు వెలువడే వికిరణ గీతలు బ్రాకెట్ శ్రేణికి చెందినవిగా పరిగణించబడతాయి. ఈ బ్రాకెట్ శ్రేణి విద్యుదయస్కాంత వర్ణపటంలో ఇన్‌ఫ్రారెడ్ (పరారుణ) ప్రాంతంలో కనబడుతుంది.

ప్రశ్న 11.సల్ఫర్ పరమాణువులో ఎన్ని p ఎలక్ట్రాన్లు ఉన్నాయి?

జవాబు:సల్ఫర్ (Z = 16) యొక్క ఎలక్ట్రాన్ విన్యాసం: 1s² 2s² 2p⁶ 3s² 3p⁴.
ఇందులో 2p ఉపఖండంలో 6 ఎలక్ట్రాన్లు, 3p ఉపఖండంలో 4 ఎలక్ట్రాన్లు ఉన్నాయి.
అందువల్ల సల్ఫర్ పరమాణువులో మొత్తం 10 p ఎలక్ట్రాన్లు ఉంటాయి.

ప్రశ్న 12.3d ఎలక్ట్రాన్ ప్రధాన క్వాంటమ్ సంఖ్య (n), ఎజిముతల్ క్వాంటమ్ సంఖ్య (7) విలువలు ఎంత?

జవాబు:3d ఎలక్ట్రాన్‌కు n = 3, l = 2.

ప్రశ్న 13.ఇచ్చిన పరమాణు సంఖ్య (Z), పరమాణు ద్రవ్యరాశి (A) గల పరమాణు పూర్తి గుర్తు ఏమిటి?

(I) Z = 4, A = 9 ; (II)Z=17, A = 35 (III) 2 = 92, A =233:

జవాబు:(I) ^9₄Be (బెరిళియమ్-9)
(II) ^35₁₇Cl (క్లోరీన్-35)
(III) ^233₉₂U (యురేనియమ్-233)

ప్రశ్న 14.dz² ఆర్బిటాల్ ఆకారాన్ని గీయండి.

జవాబు:
dz² ఆర్బిటాల్ ఆకారం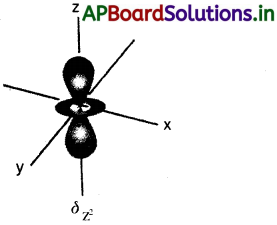

ప్రశ్న 15.dx²-y² ఆర్బిటాల్ ఆకారాన్ని గీయండి.

జవాబు:dx²-y² ఆర్బిటాల్ ఆకారం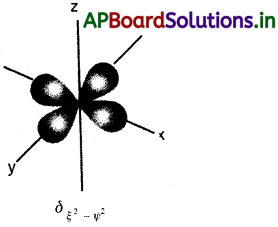

dx²-y² ఆర్బిటాల్ ఆకారం

ప్రశ్న 16.600 nm తరంగదైర్ఘ్యం గల వికిరణాల పౌనఃపున్యం ఎంత?
జవాబు:వికిరణాల పౌనఃపున్యం (ν) సూత్రం ప్రకారం,

$$\nu = \frac{c}{\lambda}$$

ఇక్కడ

• $c = 3 \times 10^8 \, m/s$ (కాంతి వేగం)

• $\lambda = 600 \, nm = 600 \times 10^{-9} \, m$

$$\nu = \frac{3 \times 10^8}{600 \times 10^{-9}} = 5 \times 10^{14} \, Hz$$

∴ 600 nm తరంగదైర్ఘ్యం గల వికిరణాల పౌనఃపున్యం $5 \times 10^{14} \, Hz$.

ప్రశ్న 17.జీమన్ ప్రభావం అంటే ఏమిటి?

జవాబు:పరమాణువును బలమైన అయస్కాంత క్షేత్రంలో ఉంచినప్పుడు, వర్ణపటంలోని ఒకే గీత అనేక సూక్ష్మ గీతలుగా విభజించబడుతుంది. ఈ పరిణామాన్ని జీమన్ ప్రభావం అని అంటారు.

ప్రశ్న 18.స్టార్క్ ప్రభావం అంటే ఏమిటి?

జవాబు:పరమాణువు బలమైన విద్యుత్ క్షేత్రంలో ఉన్నప్పుడు, దాని వర్ణపటంలోని ఒక గీత అనేక సూక్ష్మ గీతలుగా విడిపోతుంది. ఈ సంఘటనను స్టార్క్ ప్రభావం అని వ్యవహరిస్తారు.

ప్రశ్న 19.ఈ కింది ఎలక్ట్రాన్ విన్యాసాలు ఏ మూలకాలకు చెందినవి?
(I) 1s²2s²2p63s² 3p¹ (II) 1s²2s²2p63s²3p6 (III) 1s²2s²2p5 (IV) 1s²2s²2p².

జవాబు:(I) 1s²2s²2p⁶3s²3p¹ → అల్యూమినియం (Al)
(II) 1s²2s²2p⁶3s²3p⁶ → ఆర్గాన్ (Ar)
(III) 1s²2s²2p⁵ → ఫ్లోరిన్ (F)
(IV) 1s²2s²2p² → కార్బన్ (C)

ప్రశ్న 20.4000 Å తరంగదైర్ఘ్య వికిరణాలను లోహతలంపై పడేటట్లు చేస్తే శూన్యం వేగం గల ఎలక్ట్రాన్లు ఉద్గారమయ్యాయి. ఆరంభ పౌనఃపున్యం (ν0) ఎంత?

జవాబు:ఆరంభ పౌనఃపున్యం (ν₀) సూత్రం:

$$\nu_0 = \frac{c}{\lambda}$$

ఇక్కడ,

• కాంతి వేగం $c = 3 \times 10^8 \, m/s$

• తరంగదైర్ఘ్యం $\lambda = 4000 \, Å = 4000 \times 10^{-10} \, m = 4 \times 10^{-7} \, m$

$$\nu_0 = \frac{3 \times 10^8}{4 \times 10^{-7}} = 7.5 \times 10^{14} \, Hz$$

∴ ఆరంభ పౌనఃపున్యం $7.5 \times 10^{14} \, Hz$.

ప్రశ్న 21.పౌలివర్ణన సూత్రాన్ని వివరించండి.

జవాబు:పౌలి వర్జన సూత్రం ప్రకారం, ఒకే పరమాణువులోని రెండు ఎలక్ట్రాన్లకు నాలుగు క్వాంటం సంఖ్యలన్నీ ఒకే విధంగా ఉండలేవు. అంటే, ఒక ఆర్బిటల్‌లో గరిష్ఠంగా రెండు ఎలక్ట్రాన్లు మాత్రమే ఉండగలవు, అవి తప్పనిసరిగా పరస్పర విరుద్ధ స్పిన్‌లను కలిగి ఉండాలి.

ప్రశ్న 22.ఆఫ్ నియమం అంటే ఏమిటి?

జవాబు:ఆఫ్ బౌ నియమం ప్రకారం, ఎలక్ట్రాన్లు పరమాణువు భూస్థితిలో (ground state) ఉన్నప్పుడు తక్కువ శక్తి గల ఆర్బిటల్స్‌లో ముందుగా చేరతాయి. శక్తి క్రమంగా పెరుగుతున్న ఆర్బిటల్స్ తర్వాత తర్వాత ఎలక్ట్రాన్లతో నిండి పోతాయి.

అంటే, ఆర్బిటల్స్ ఎలక్ట్రాన్లతో భర్తీ కావడం శక్తి స్థాయి పెరుగుతున్న క్రమంలో జరుగుతుంది.

ప్రశ్న 23.హుండ్ నియమం అంటే ఏమిటి?

జవాబు:హుండ్ నియమం ప్రకారం, సమాన శక్తి కలిగిన (డీజనరేట్) ఆర్బిటల్స్ ఎక్కువగా ఉన్నప్పుడు, మొదట ప్రతి ఆర్బిటల్‌లో ఒక్కో ఎలక్ట్రాన్ చొప్పున నింపబడుతుంది. ఆ తరువాత మాత్రమే ఎలక్ట్రాన్లు జతగా ప్రవేశిస్తాయి.

అందువల్ల, డీజనరేట్ ఆర్బిటల్స్‌లో ఎలక్ట్రాన్ల విభజన గరిష్ఠ స్థిరత్వాన్ని కలిగించే విధంగా జరుగుతుంది.

ప్రశ్న 24.హైసన్బర్గ్ అనిశ్చితత్వ నియమం వివరించండి.

జవాబు:హైసెన్బర్గ్ అనిశ్చితత్వ సూత్రం ప్రకారం, ఎలక్ట్రాన్ వంటి సూక్ష్మ పరమాణు కణం యొక్క స్థానం (∆x) మరియు ద్రవ్యవేగం (∆p) రెండింటినీ ఒకేసారి ఖచ్చితంగా నిర్ణయించడం అసాధ్యం.

ఈ సూత్రాన్ని గణితరూపంలో ఇలా వ్రాయవచ్చు:

$$\Delta x \cdot \Delta p \geq \frac{h}{4\pi}$$

ఇక్కడ $h$ = ప్లాంక్ స్థిరాంకం.

హైసెన్బర్గ్ నియమ ప్రాముఖ్యత:

• ఎలక్ట్రాన్ వంటి కణాలకు స్థిరమైన కక్ష్యలు లేదా ఖచ్చితమైన ప్రక్షేప మార్గం ఉండవు.

• ఈ సూత్రం సూక్ష్మ కణాలకు మాత్రమే వర్తిస్తుంది; స్థూల వస్తువులకు దాని ప్రభావం ఉండదు.

• మిల్లీగ్రామ్ లేదా అంతకంటే ఎక్కువ బరువున్న వస్తువులకు అనిశ్చితత్వ ప్రభావం పట్టించుకోదగ్గది కాదు.

ప్రశ్న 25.2.0 × 107m/s-1 వేగంతో ప్రయాణించే ఎలక్ట్రాన్ తరంగదైర్ఘ్యం ఎంత?

జవాబు:ఎలక్ట్రాన్ తరంగదైర్ఘ్యం డి బ్రాగ్లి సూత్రం ద్వారా లెక్కించబడుతుంది:

$$\lambda = \frac{h}{mv}$$

ఇక్కడ

• $h = 6.626 \times 10^{-34} \, J \cdot s$ (ప్లాంక్ స్థిరాంకం)

• $m = 9.11 \times 10^{-31} \, kg$ (ఎలక్ట్రాన్ ద్రవ్యం)

• $v = 2.0 \times 10^7 \, m/s$ (ఎలక్ట్రాన్ వేగం)

$$\lambda = \frac{6.626 \times 10^{-34}}{(9.11 \times 10^{-31})(2.0 \times 10^7)}$$ $$\lambda = 3.63 \times 10^{-11} \, m$$

∴ ఎలక్ట్రాన్ తరంగదైర్ఘ్యం $3.63 \times 10^{-11} \, m$.

ప్రశ్న 26.పరమాణు ఆర్బిటాల్కు n విలువ 2 అయిన I, m,లకు సాధ్యమైన విలువలేమి ?

జవాబు:
n = 2 అయిన = 0,1
l = 0 అయిన ml = 0
l = 1 అయిన ml = -1, 0, +1

ప్రశ్న 27.ఇక్కడ ఇచ్చిన ఆర్బిటాల్లో ఏవి సాధ్యం? 2s, 1p, 3f, 2p.

జవాబు:ఇచ్చిన ఆర్బిటల్స్‌లో 2s మరియు 2p మాత్రమే సాధ్యమైనవి. 1p మరియు 3f ఆర్బిటల్స్ అసంభవమైనవి.

కారణము :
రెండవ శక్తిస్థాయిలో (n = 2) రెండు ఉపశక్తి స్థాయిలుంటాయి. అవి. l = 0(s) మరియు 1(p) వాటిని ‘2s’ మరియు ‘2p’ గా సూచిస్తారు.

ప్రశ్న 28.నూనె చుక్క మీద ఉన్న స్థిర విద్యుత్ ఆవేశం – 3.2044 × 10-19 C. దానిమీద ఎన్ని ఎలక్ట్రాన్లు ఉన్నాయి?

జవాబు:ఇచ్చినవి:

• నూనె చుక్క మొత్తం ఆవేశం $Q = 3.2044 \times 10^{-19} \, C$

• ఒక ఎలక్ట్రాన్ ఆవేశం $e = 1.602 \times 10^{-19} \, C$

ఎలక్ట్రాన్ల సంఖ్య:

$$n = \frac{Q}{e} = \frac{3.2044 \times 10^{-19}}{1.602 \times 10^{-19}}$$ $$n = 2$$

∴ నూనె చుక్కపై 2 ఎలక్ట్రాన్లు ఉన్నాయి.

ప్రశ్న 29.కింద ఇచ్చిన వికిరణాలను పౌనఃపున్యాలు పెరిగే క్రమంలో ఏర్పరచండి.
(a) × – కిరణాలు
(b) దృగ్గోచర వికిరణాలు
(c) సూక్ష్మతరంగ వికిరణాలు
(d) రేడియో తరంగ వికిరణాలు

జవాబు:రేడియో తరంగాలు < సూక్ష్మతరంగ వికిరణాలు < దృగ్గోచర వికిరణాలు < ఎక్స్ – కిరణాలు

ప్రశ్న 30.n = 4, ms = + 1/2 తో పరమాణువులో ఉండే ఎలక్ట్రాన్ల సంఖ్య ఎంత?
జవాబు:

• ప్రధాన క్వాంటం సంఖ్య n = 4 ఉన్నప్పుడు, l విలువలు 0, 1, 2, 3 అవుతాయి.

• l = 0 (4s) ఆర్బిటల్ → ms = +1/2 తో 1 ఎలక్ట్రాన్.

• l = 1 (4p) ఆర్బిటల్స్ (మొత్తం 3) → ఒక్కో ఆర్బిటల్‌లో ms = +1/2 తో 1 ఎలక్ట్రాన్ → 3 ఎలక్ట్రాన్లు.

• l = 2 (4d) ఆర్బిటల్స్ (మొత్తం 5) → ఒక్కో ఆర్బిటల్‌లో ms = +1/2 తో 1 ఎలక్ట్రాన్ → 5 ఎలక్ట్రాన్లు.

• l = 3 (4f) ఆర్బిటల్స్ (మొత్తం 7) → ఒక్కో ఆర్బిటల్‌లో ms = +1/2 తో 1 ఎలక్ట్రాన్ → 7 ఎలక్ట్రాన్లు.

∴ మొత్తం ఎలక్ట్రాన్ల సంఖ్య = 1 + 3 + 5 + 7 = 16 ఎలక్ట్రాన్లు.

ప్రశ్న 31.n = 5 లో ఉండే ఉపకర్పరాల సంఖ్య ఎంత?

జవాబు:n = 5 అయినప్పుడు l విలువలు 0, 1, 2, 3, 4 అవుతాయి.

• l = 0 → s – ఆర్బిటాల్

• l = 1 → p – ఆర్బిటాల్

• l = 2 → d – ఆర్బిటాల్

• l = 3 → f – ఆర్బిటాల్

• l = 4 → g – ఆర్బిటాల్

అందువల్ల, n = 5 లో 5 ఉపకర్పరాలు ఉంటాయి.

ప్రశ్న 32.విద్యుదయస్కాంత వికిరణాల కణస్వభావాన్ని వివరించండి.

జవాబు:న్యూటన్ తన సిద్ధాంతంలో కాంతి అనేది సూక్ష్మ కణాల వలయంగా ఏర్పడిందని పేర్కొన్నాడు. ఈ కణాలను కార్పస్కుల్స్ అని పిలిచాడు.

కాంతి కణస్వభావం ద్వారా కృష్ణవస్తువు వికిరణం మరియు ప్రకాశ విద్యుత్ ప్రభావం వంటి అంశాలను విజయవంతంగా వివరించగలిగారు.
అయితే, ఈ కణస్వభావం ద్వారా వివర్తనం మరియు వ్యతికరణం వంటి తరంగ సంబంధిత లక్షణాలను వివరించడం సాధ్యం కాలేదు.

ప్రశ్న 33.హైసన్బర్గ్ అనిశ్చితత్వ నియమం ప్రాముఖ్యాన్ని వివరించండి.

జవాబు:హైసన్బర్గ్ అనిశ్చితత్వ సూత్రం ప్రకారం, ఎలక్ట్రాన్ వంటి సూక్ష్మకణానికి ఒకేసారి ఖచ్చితమైన స్థానం మరియు వేగం (గతి పరిమాణం) తెలియజేయడం అసాధ్యం.
ఈ సూత్రం వల్ల ఎలక్ట్రాన్ స్థిరమైన కక్ష్యలో తిరుగుతుందనే బోర్ మోడల్ ఆలోచన సరిపోదని నిర్ధారణ అయింది.
ఇది ప్రధానంగా సూక్ష్మ స్థాయి కణాలకు మాత్రమే వర్తిస్తుంది; పెద్ద పరిమాణం గల వస్తువులకు ఈ ప్రభావం లెక్కలోకి తీసుకోదగినంత చిన్నది కాబట్టి ప్రాముఖ్యం ఉండదు.

ప్రశ్న 34.హైడ్రోజన్ వర్ణపటంలో పరిశీలించిన రేఖ శ్రేణులు ఏమిటి ?

జవాబు:

• n = 1 → లైమన్ శ్రేణి – అల్ట్రావయొలెట్ (UV) ప్రాంతంలో ఉంటుంది.

• n = 2 → బామర్ శ్రేణి – కంటికి కనిపించే (Visible) ప్రాంతంలో ఉంటుంది.

• n = 3 → పాషెన్ శ్రేణి – ఇన్‌ఫ్రారెడ్ (IR) ప్రాంతంలో ఉంటుంది.

• n = 4 → బ్రాకెట్ శ్రేణి – ఇన్‌ఫ్రారెడ్ (IR) ప్రాంతంలో ఉంటుంది.

• n = 5 → ఫండ్ శ్రేణి – ఇన్‌ఫ్రారెడ్ (IR) ప్రాంతంలో ఉంటుంది.

స్వల్ప సమాధాన ప్రశ్నలు

ప్రశ్న 1.హైడ్రోజన్ పరమాణువులో ఎలక్ట్రాన్ n = 5 శక్తి స్థాయి నుంచి n = 3 శక్తి స్థాయికి పరివర్తనం n = చెందినప్పుడు ఉద్గారమయ్యే కాంతి తరంగదైర్ఘ్యం ఎంత?

జవాబు:ఇచ్చిన సమాచారం:

• రైడ్‌బర్గ్ స్థిరాంకం, R = 1.09677 × 10⁵ cm⁻¹

• n₁ = 3

• n₂ = 5

సూత్రం:

$$\bar{\nu} = R \left(\frac{1}{n_1^2} - \frac{1}{n_2^2}\right)$$ $$\bar{\nu} = 1.09677 × 10^5 \left(\frac{1}{3^2} - \frac{1}{5^2}\right)$$ $$\bar{\nu} = 1.09677 × 10^5 \left(\frac{1}{9} - \frac{1}{25}\right)$$ $$\bar{\nu} = 1.09677 × 10^5 \left(\frac{25 - 9}{225}\right)$$ $$\bar{\nu} = 1.09677 × 10^5 \times \frac{16}{225}$$ $$\bar{\nu} = 7799.25 \, cm^{-1}$$

తరంగదైర్ఘ్యం:

$$\lambda = \frac{1}{\bar{\nu}} = \frac{1}{7799.25} \, cm = 1.28 × 10^{-4} cm = 1282 \, nm$$

అందువల్ల ఉద్గారమయ్యే కాంతి తరంగదైర్ఘ్యం ≈ 1282 nm (ఇన్‌ఫ్రారెడ్ ప్రాంతం).

ప్రశ్న 2.ఒక మూలకపు పరాణువులో 29 ఎలక్ట్రాన్లు, 35 న్యూట్రాన్లు ఉన్నాయి.
i) ప్రోటాన్ల సంఖ్యను,
ii) మూలకం ఎలక్ట్రాన్ విన్యాసాన్ని రాబట్టండి.

జవాబు:
ఎలక్ట్రాన్ల సంఖ్య 29 ఇవ్వబడినది
i) ప్రోటాన్ ల సంఖ్య = 29
ii) 2 = 29, మూలకం ‘Cu’
ఎలక్ట్రాన్ విన్యాసం = 1s² 2s² 2p² 3s² 3p64s¹ 3d10

ప్రశ్న 3.
ఈ కింది క్వాంటమ్ సంఖ్యల సమితులు అసాధ్యమైనవేవి ? కారణాలతో వివరించండి.
(a) n = 0, l = o, ml = 0, ms = +12
(b) n = 1, l = 0, ml = 0, ms = –12
(c) n = 1, l = 1, ml = 0, ms = +12
(d) n = 2, l = 1, ml = 0, ms = +12
(e) n = 3, l = 3, ml = -3, ms = +12
(f) n = 3, l = 1, ml = 0, ms = +12
జవాబు:
ఈ క్రింది క్వాంటమ్ సంఖ్యల సమితులు సాధ్యం కావు.

a) n = 0, 1 = 0, ml = 0, ms = +12
కారణము :
ప్రధాన క్వాంటమ్ సంఖ్య (n) విలువలు 1 నుంచి n వరకు ఉంటాయి ‘n’ కు సున్న విలువ ఉండదు కాని n = 0 అని ఇవ్వబడినది.

c) n = 1, l = 1, ml = 0, ms = +12
కారణము :
‘l’ విలువలు 0 నుండి (n – 1) వరకు ఉంటాయి.
అంటే n = 1 అయితే l = 0 అవుతుంది. కానీ ‘1’ అవ్వదు.

e) n = 3, l = 3, m, = -3, ms = +12
కారణము :
n = 3, కి ‘l’ విలువలు 0, 1, 2, అవుతాయి కాని ‘3’ అవ్వదు.

ప్రశ్న 4.హైడ్రోజన్ పరమాణువు బోర్ కక్ష్యలో తిరుగుతున్న ఎలక్ట్రాన్ కక్ష్య చుట్టుకొలత డీబ్రోలీ తరంగదైర్ఘ్యానికి పూర్ణాంక గుణిజంగా ఉంటుందని చూపించండి.

జవాబు:సమాధానం (సరళీకృత ప్రూఫ్):

1. డీబ్రోలీ సూత్రం ప్రకారం ఒక ద్రవ్య కణానికి తరంగదైర్ఘ్యం

$$\lambda = \frac{h}{p} = \frac{h}{mv}$$

ఇక్కడ $h$ = ప్లాంక్ స్థిరాంకం, $m$ = ఎలక్ట్రాన్ ద్రవ్యరాశి, $v$ = వేగం.

2. బోర్ మోడల్‌లో ఎన్నివిధంగా క్వాంటైజ్డ్ యాంగ్యులర్ మోమెంటం ఉంటుందో:

$$m v r = \frac{n h}{2\pi}$$

ఇక్కడ $r$ = కక్ష్యత్రిజ్య, $n$ = ధనాత్మక పూర్తి సంఖ్య (1,2,3,...).

3. పై సమీకరణను పునర్వ్యవహరించి $2\pi r$ కోసం వేశారు:

$$2\pi r = \frac{n h}{m v}$$

4. ఇప్పుడు డీబ్రోలీ ఇవ్వటం ($\lambda=\frac{h}{mv}$)ని (3) లో ప్రత్యామ్నాయంగా ఉంచులు:

$$2\pi r = n\left(\frac{h}{mv}\right) = n\lambda$$

కాబట్టి బోర్ ఆర్బిట్ చుట్టు వ్యాసార్ధం (సర్కమ్మిఫరెన్స్) $2\pi r$ = $n\lambda$. అర్థం: ఎలక్ట్రాన్ కక్ష్య చుట్టు ఉండే స్థానం డీబ్రోలీ తరంగదైర్ఘ్య యొక్క పూర్ణాంక గుణకంగా ఉండాలి.

భౌతిక అర్థం: ఇది ఆర్బిట్‌లో స్థిరమైన నిలిచి ఉండే (standing) తరంగాన్ని సూచిస్తుంది — ఒక సరిగ్గా పనిచేసే స్థావర తరంగం కావాలంటే కక్ష్యపాతది మొత్తానికి పూర్తి సంఖ్య వంటి అర్ధ వేవ్‌లు సరిపోయినాలి. దానివల్లే బోర్ యొక్క క్వాంటైజేషన్ నిచ్చెనకు డీబ్రోలీ ధారణ ఒక ప్రకృతి సంబంధిత వివరణను ఇస్తుంది.

ప్రశ్న 5.589.0, 589.6 mm లు గరిష్ఠ ద్వంద్వ శోషణ పరివర్తన తరంగదైర్ఘ్యాలుగా పరిశీలించబడ్డాయి. పరివర్తన పౌనఃపున్యాలను, రెండు ఉత్తేజస్థితుల మధ్య శక్తి తేడాలను లెక్కించండి.జవాబు:ఉపయోగించిన స్థిరాంకాలు (సరళీకృతంగా) :

$c = 2.99792458\times10^8\ \text{m·s}^{-1}$ , $h = 6.62607015\times10^{-34}\ \text{J·s}$ , $1\ \text{eV} = 1.602176634\times10^{-19}\ \text{J}$.

1. $\lambda_1 = 589.0\ \text{nm} = 589.0\times10^{-9}\ \text{m}$

$$\nu_1=\frac{c}{\lambda_1}=\frac{2.99792458\times10^8}{589.0\times10^{-9}} \approx 5.0899\times10^{14}\ \text{Hz}$$

శక్తి $E_1 = h\nu_1 \approx 6.62607015\times10^{-34}\times5.0899\times10^{14} \approx 3.3726\times10^{-19}\ \text{J}$
అన్ని-వేలిలో: $E_1 \approx \dfrac{3.3726\times10^{-19}}{1.602176634\times10^{-19}}\approx 2.104\ \text{eV}$.

2. $\lambda_2 = 589.6\ \text{nm} = 589.6\times10^{-9}\ \text{m}$

$$\nu_2=\frac{c}{\lambda_2}\approx 5.0847\times10^{14}\ \text{Hz}$$

శakti $E_2 = h\nu_2 \approx 6.62607015\times10^{-34}\times5.0847\times10^{14} \approx 3.3691\times10^{-19}\ \text{J}$
అన్ని-వేలిలో: $E_2 \approx 2.102\ \text{eV}$.

3. రెండు మధ్య శక్తి తేడా:

$$\Delta E = |E_1 - E_2| \approx 3.3726\times10^{-19} - 3.3691\times10^{-19} \approx 3.43\times10^{-22}\ \text{J}$$

ఎలెక్ట్రాన్‌వోల్టులో:

$$\Delta E \approx \frac{3.43\times10^{-22}}{1.602176634\times10^{-19}} \approx 2.14\times10^{-3}\ \text{eV} \;(=0.00214\ \text{eV})$$

సంక్షిప్తంగా అంతిమ ఫలితాలు:

• $\nu_1(589.0\ \text{nm}) \approx 5.0899\times10^{14}\ \text{Hz},\; E_1 \approx 3.3726\times10^{-19}\ \text{J}\ (2.104\ \text{eV})$.

• $\nu_2(589.6\ \text{nm}) \approx 5.0847\times10^{14}\ \text{Hz},\; E_2 \approx 3.3691\times10^{-19}\ \text{J}\ (2.102\ \text{eV})$.

• శక్తి తేడా $\Delta E \approx 3.43\times10^{-22}\ \text{J} \approx 2.14\times10^{-3}\ \text{eV}$.

ప్రశ్న 7.పరమాణువు క్వాంటమ్ యాంత్రిక నమూనా ముఖ్య లక్షణాలు ఏమిటి?

జవాబు:పరమాణువు యొక్క క్వాంటమ్ యాంత్రిక నమూనా క్రింది ప్రధాన లక్షణాలను వివరిస్తుంది –

1. శక్తి క్వాంటీకరణం – పరమాణువులో ఎలక్ట్రాన్ల శక్తి నిర్దిష్టమైన క్వాంటీకృత స్థాయిల్లో మాత్రమే ఉంటుంది.

2. తరంగ స్వభావం – ఎలక్ట్రాన్లకు తరంగ స్వభావం ఉండటం వల్ల, అవి నిర్దిష్ట శక్తి స్థితుల్లోనే నిలదొక్కుకుంటాయి.

3. ఆర్బిటల్ తరంగ ప్రమేయం (Ψ) – పరమాణువులోని ఎలక్ట్రాన్ సమాచారమంతా తరంగ ప్రమేయం Ψ లో ఉంటుంది.

4. హైజన్బర్గ్ అనిశ్చితి సూత్రం – ఎలక్ట్రాన్ యొక్క ఖచ్చితమైన స్థానం, మార్గం తెలుసుకోవడం సాధ్యం కాదు. కేవలం దాని సంభావ్యతను మాత్రమే అంచనా వేయగలము.

5. సంభావ్యతా సాంద్రత (Ψ²) – ఒక నిర్దిష్ట బిందువులో ఎలక్ట్రాన్ ఉండే అవకాశాన్ని Ψ² సూచిస్తుంది. ఇది ఎల్లప్పుడూ ధన విలువే అవుతుంది.

6. గరిష్ట సంభావ్యతా ప్రాంతం – Ψ² విలువల ఆధారంగా ఎలక్ట్రాన్ ఉండే గరిష్ట అవకాశమున్న ప్రాంతాన్ని గుర్తించవచ్చు.

ప్రశ్న 8.నోడల్ తలం అంటే ఏమిటి? 2p, 3d – ఆర్బిటాల్లలో ఎన్ని నోడల్ తలాలుంటాయి?
జవాబు:

• నోడల్ తలం (Nodal Plane):
  ఎలక్ట్రాన్‌ను కనుగొనే సంభావ్యత పూర్తిగా శూన్యం (Ψ² = 0) అయ్యే స్థలాన్ని నోడల్ తలం అంటారు.
  ఇది ఆర్బిటాల్‌లోని దిశలు లేదా ఉపరితలాల మీద ఉంటుంది.

• ఒక ఆర్బిటాల్‌లోని నోడల్ తలాల సంఖ్య = l విలువ (ఆర్బిటాల్ యొక్క అజిముతల్ క్వాంటం సంఖ్య).

ఉదాహరణలు :

• 2p ఆర్బిటాల్ (l = 1) → నోడల్ తలాలు = 1

• 3d ఆర్బిటాల్ (l = 2) → నోడల్ తలాలు = 2 ✅

👉 కాబట్టి,
2p – ఆర్బిటాల్ → 1 నోడల్ తలం
3d – ఆర్బిటాల్ → 2 నోడల్ తలాలు

ప్రశ్న 9.91.2 nm నుంచి 121.6 nm ల మధ్య లైమన్ శ్రేణి, 364.7 nm నుంచి 656.5 nm ల మధ్య బామర్శ్రేణి, 820.6 nm నుంచి 1876 pm ల మధ్య పాశ్చన్ శ్రేణి కనబడతాయి. ఈ తరంగదైర్ఘ్యాలు వర్ణపటంలో ఏ ప్రాంతానికి చెందినవో కనుక్కోండి.

జవాబు:విద్యుదయస్కాంత వర్ణపటంలో –

1. లైమన్ శ్రేణి (91.2 – 121.6 nm): ఇది అతినీలలోహిత (Ultraviolet) ప్రాంతంలో ఉంటుంది.

2. బామర్ శ్రేణి (364.7 – 656.5 nm): ఇది దృశ్య (Visible) ప్రాంతంలో ఉంటుంది.

3. పాశ్చన్ శ్రేణి (820.6 – 1876 nm): ఇది పరారుణ (Infrared) ప్రాంతంలో ఉంటుంది. ✅

ప్రశ్న 10.హైడ్రోజన్ పరమాణువులో n. l, m, క్వాంటమ్ సంఖ్యలు ఎలా వస్తాయి?

జవాబు:హైడ్రోజన్ పరమాణువు యొక్క ఎలక్ట్రాన్ విన్యాసం 1s¹.

అందువలన దాని ఎలక్ట్రాన్‌కు క్వాంటమ్ సంఖ్యలు ఇలా ఉంటాయి –

• ప్రధాన క్వాంటమ్ సంఖ్య (n): $n = 1$

• కోణీయ క్వాంటమ్ సంఖ్య (l): $l = 0$ (s-ఆర్బిటల్‌కు)

• చుంబక క్వాంటమ్ సంఖ్య (mₗ): $mₗ = 0$

• స్పిన్ క్వాంటమ్ సంఖ్య (mₛ): $mₛ = +\tfrac{1}{2}$ లేదా $-\tfrac{1}{2}$

👉 కాబట్టి హైడ్రోజన్ పరమాణువు ఎలక్ట్రాన్‌కు క్వాంటమ్ సంఖ్యల సమితి:
$(n, l, m_l, m_s) = (1, 0, 0, +\tfrac{1}{2})$ లేదా $(1, 0, 0, -\tfrac{1}{2})$. ✅

ప్రశ్న 11.హైడ్రోజన్ పరమాణువులో లైమన్ శ్రేణిలో ఒక రేఖ తరంగదైర్ఘ్యం 1.03 × 10-7 m అయితే ఎలక్ట్రాన్ తొలి శక్తిస్థాయి ఏది?

జవాబు:దత్తాంశము:

$$\lambda = 1.03 \times 10^{-7}\, m = 1.03 \times 10^{-5}\, cm$$

లైమన్ శ్రేణిలో $\,n_1 = 1$

$$R = 109677\, cm^{-1}$$

సూత్రం:

$$\frac{1}{\lambda} = R \left( \frac{1}{n_1^2} - \frac{1}{n_2^2} \right)$$ $$\frac{1}{1.03 \times 10^{-5}} = 109677 \left(1 - \frac{1}{n_2^2}\right)$$ $$97087 = 109677 \left(1 - \frac{1}{n_2^2}\right)$$ $$\frac{97087}{109677} = 1 - \frac{1}{n_2^2}$$ $$0.885 = 1 - \frac{1}{n_2^2}$$ $$\frac{1}{n_2^2} = 0.115$$ $$n_2^2 \approx 8.7$$ $$n_2 \approx 3$$

---

✅ కాబట్టి ఎలక్ట్రాన్ తొలి శక్తిస్థాయి $n_2 = 3$.

ప్రశ్న 12.ఎలక్ట్రాన్ స్థితిని ±0.002 nm లోపు కచ్చితంగా కొలవగలిగినట్లైతే ఎలక్ట్రాన్ ద్రవ్యవేగంలో అనిశ్చితత్వం గణించండి.
జవాబు:దత్తం :

$$\Delta x = 0.002 \, nm = 0.002 \times 10^{-9} \, m = 2 \times 10^{-12} \, m$$

హైసెన్‌బర్గ్ అనిశ్చితత్వ సూత్రం ప్రకారం –

$$\Delta x \cdot \Delta p \geq \frac{h}{4 \pi}$$

ఇక్కడ
$\Delta p = m \Delta v$

అందువలన,

$$\Delta v = \frac{h}{4 \pi m \Delta x}$$

ఇక్కడ,
$h = 6.626 \times 10^{-34} \, Js$
$m = 9.11 \times 10^{-31} \, kg$
$\Delta x = 2 \times 10^{-12} \, m$

$$\Delta v = \frac{6.626 \times 10^{-34}}{4 \pi \times 9.11 \times 10^{-31} \times 2 \times 10^{-12}}$$ $$\Delta v = \frac{6.626 \times 10^{-34}}{2.29 \times 10^{-41}}$$ $$\Delta v \approx 2.89 \times 10^{7} \, m/s$$

అందువలన, ఎలక్ట్రాన్ వేగంలో అనిశ్చితత్వం $\mathbf{2.9 \times 10^{7} \, m/s}$. ✅

ప్రశ్న 13.1.6 × 106 m/s-1 ఎలక్ట్రాన్ వేగం ఉన్నట్లయితే దానితో ఉన్న డీబ్రోలీ తరంగదైర్ఘ్యాన్ని గణించండి.

జవాబు:ఇవ్వబడినవి :

ఎలక్ట్రాన్ వేగం (v) = 1.6 × 10⁶ m/s
ఎలక్ట్రాన్ ద్రవ్యరాశి (m) = 9.1 × 10⁻³¹ kg
ప్లాంక్ స్థిరాంకం (h) = 6.626 × 10⁻³⁴ J·s

సూత్రం:

$$\lambda = \frac{h}{mv}$$

గణన:

$$\lambda = \frac{6.626 \times 10^{-34}}{(9.1 \times 10^{-31})(1.6 \times 10^6)}$$ $$\lambda = \frac{6.626 \times 10^{-34}}{1.456 \times 10^{-24}}$$ $$\lambda = 4.55 \times 10^{-10}\, \text{m}$$

ఫలితం:
ఎలక్ట్రాన్ యొక్క డీ–బ్రోగ్లీ తరంగదైర్ఘ్యం

$$\lambda = 4.55 × 10^{-10}\, \text{m}$$

👉 దీన్ని 0.455 nm గా కూడా వ్రాయవచ్చు.

ప్రశ్న 14.శోషణ, ఉద్గార వర్ణపటాల మధ్య తేడాలను వివరించండి. [AP.Mar. ’15]
జవాబు:

ఉద్గార వర్ణపటం	శోషణ వర్ణపటం
1. ఇది అణువు లేదా అయాన్ శక్తిని విడుదల చేసినప్పుడు ఏర్పడుతుంది.	1. ఇది అణువు లేదా అయాన్ శక్తిని శోషించినప్పుడు ఏర్పడుతుంది.
2. నలుపు నేపథ్యంపై ప్రకాశవంతమైన గీతలు కనిపిస్తాయి.	2. ప్రకాశవంతమైన నేపథ్యంపై నల్లటి గీతలు కనిపిస్తాయి.
3. ఎలక్ట్రాన్ పై స్థాయి నుండి క్రింది స్థాయికి పడినప్పుడు ఏర్పడుతుంది.	3. ఎలక్ట్రాన్ క్రింది స్థాయి నుండి పై స్థాయికి ఎగిరినప్పుడు ఏర్పడుతుంది.

👉 సరళంగా చెప్పాలంటే, ఉద్గార వర్ణపటంలో కాంతి విడుదల అవుతుంది, శోషణ వర్ణపటంలో కాంతి తీయబడుతుంది.

ప్రశ్న 15.ఎలక్ట్రాన్ల క్వాంటమ్ సంఖ్యలు కింద ఇవ్వడమైంది. వాటిని శక్తిపరంగా ఆరోహణ క్రమంలో రాయండి.
(a) n = 4, l = 2, ml = -2, ms = +12
(b) n = 3, l = 2, ml = -1, ms = –12
(c) n = 4, l = 1, ml = 0, ms = +12
(d) n = 3, l = 2, ml = -1, ms = –12
జవాబు:
ఆర్బిటాల్ యొక్క శక్తికి ఫార్ములా (n + 1)
∴ ఇవ్వబడిన ప్రతి సంయోగానికి (n + 1) విలువలు
(1) కి n + l = 4 + 2 = 6
(2) కి n + l = 3 + 2 = 5
(3) కి n + l = 4 + 1 = 5
(4) కి n + l = 3 + 2 = 5
(5) కి n + l = 3+1 = 4
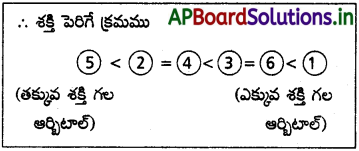
(6) కి n + 1 = 4+1 = 5

• (n + 1) విలువ తక్కువ ఉంటే, ఆ స్థాయి శక్తి తక్కువ.
• (n + l) విలువలు సమానంగా ఉన్నప్పుడు, దేనికైతే తక్కువ ‘n’ విలువ ఉంటుందో ఆ ఆర్బిటాల్ యొక్క శక్తి తక్కువ.

ప్రశ్న 16.సీజియం పరమాణువు పని ప్రమేయం 1.9 eV. ఆరంభ వికిరణాల పౌనఃపున్యాన్ని గణించండి. సీజియం మూలకాన్ని 500 nm ల తరంగదైర్ఘ్యం గల వికిరణాలతో ఉద్యోతనం (irradiation) చేస్తే వెలువడే ఫోటో ఎలక్ట్రాన్ గతిజశక్తి గణించండి.

జవాబు:స్వల్ప, విభజిత సమాధానం (వేరే రూపంలో):

1) పని ప్రమేయం నుండి ఆరంభ పౌనఃపున్య (threshold frequency $\nu_0$)

• పని ప్రమేయం $w = 1.9\ \text{eV} = 1.9\times1.602176634\times10^{-19}\ \text{J} = 3.04414\times10^{-19}\ \text{J}$.

• ప్లాంక్ స్థిరాంకం $h = 6.62607015\times10^{-34}\ \text{J·s}$.

• $\displaystyle \nu_0=\frac{w}{h}=\frac{3.04414\times10^{-19}}{6.62607\times10^{-34}}\approx 4.59\times10^{14}\ \text{Hz}.$

(అవలంభంగా, threshold wavelength $\lambda_0=\dfrac{c}{\nu_0}\approx 6.525\times10^{-7}\ \text{m}=652.5\ \text{nm}$.)

2) $500\ \text{nm}$ కాంతి ఫోటోన్ శక్తి

• $\lambda = 500\ \text{nm} = 5.00\times10^{-7}\ \text{m}$.

• కాంతి తరంగపున్యం $\nu = c/\lambda = 2.99792458\times10^{8}/5.00\times10^{-7}\approx 5.99585\times10^{14}\ \text{Hz}.$

• ఫోటాన్ శక్తి $E_{\text{ph}} = h\nu \approx 6.62607\times10^{-34}\times5.99585\times10^{14} \approx 3.97289\times10^{-19}\ \text{J} \approx 2.48\ \text{eV}.$

3) గరిష్ఠ ఫోటోఎలక్ట్రాన్ శక్తి (K$_\text{max}$) — ఫోటోఎఫెక్ట్ సమীকరణ ప్రకారం

$$h\nu = w + K_{\text{max}} \quad\Rightarrow\quad K_{\text{max}} = h\nu - w$$

• $K_{\text{max}} = 3.97289\times10^{-19}\ \text{J} - 3.04414\times10^{-19}\ \text{J} = 9.2876\times10^{-20}\ \text{J}.$

• ఇది ఎలెక్ట్రాన్‌వోల్టుల్లో $= \dfrac{9.2876\times10^{-20}}{1.602176634\times10^{-19}}\approx 0.580\ \text{eV}.$

సంక్షిప్త ఫలితాలు:

• ఆరంభ పౌనఃపున్యం (threshold frequency) $\nu_0 \approx 4.59\times10^{14}\ \text{Hz}$.

• threshold wavelength $\lambda_0 \approx 652.5\ \text{nm}$. (అర్థం: 500 nm ఈ విలువకంటే చిన్నదైనందున ఫోటోఎలక్ట్రాన్‌లు ఉద్గారమవుతాయి.)

• వెలువడే ఫోటోఎలక్ట్రాన్ గరిష్ఠ శక్తి $K_{\text{max}} \approx 9.29\times10^{-20}\ \text{J} \approx 0.580\ \text{eV}.$

ప్రశ్న 17.1.3225 nm వ్యాసార్థం గల కక్ష్యలో మొదలై 211.6 pm వ్యాసార్థం గల కక్ష్యలో చేరినట్లయితే ఉద్గార పరివర్తన తరంగదైర్ఘ్యాన్ని గణించండి. ఈ పరివర్తన ఏ శ్రేణికి చెందుతుంది ? అది వర్ణపటంలో “ఏ ప్రాంతానికి చెందుతుంది?
జవాబు:జవాబు (మరొక విధంగా):

1. మొదట ఇచ్చిన వ్యాసార్థాల నుండి సంబంధిత బోర్ శ్రేణులాన్ని నిర్ణయిస్తాం. బోర్ కక్ష్యత్రిజ్యకు సంబంధించి

$$r_n = 0.529\,\text{\AA}\times n^2.$$

• ప్రారంభ వర్గం: $r = 1.3225\ \text{nm} = 13.225\ \text{\AA}$.

  $$n^2=\dfrac{13.225}{0.529}=25\quad\Rightarrow\quad n=5.$$

• చివరి వర్గం: $r = 211.6\ \text{pm}=0.2116\ \text{nm}=2.116\ \text{\AA}$.

  $$n^2=\dfrac{2.116}{0.529}=4\quad\Rightarrow\quad n=2.$$

అర్థం: పరివర్తనం n = 5 → n = 2.

2. ఈ పరివర్తనం ఇచ్చే వెలుగు తరంగదైర్ఘ్యాన్ని రైడ్బర్గ్ సూత్రం ద్వారా లెక్కిస్తాము:

$$\bar{\nu}=R\!\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right),$$

ఇక్కడ $R=1.09677\times10^7\ \text{m}^{-1}$, $n_1=2,\; n_2=5$.

$$\bar{\nu}=1.09677\times10^7\left(\frac{1}{4}-\frac{1}{25}\right)=2.303217\times10^6\ \text{m}^{-1}.$$

ఎప్పుడు $\lambda=\dfrac{1}{\bar{\nu}}$:

$$\lambda=\dfrac{1}{2.303217\times10^6}=4.34175\times10^{-7}\ \text{m}=434.2\ \text{nm\,(పరిసర)}.$$

3. శ్రేణి మరియు వర్ణపట స్థానము:

• ఇది బామర్ (Balmer) శ్రేణి (ఎందుకంటే చివరి స్థాయి $n=2$).

• $\lambda\approx 434.2\ \text{nm}$ కావటున ఇది దృశ్య (Visible) ప్రాంతానికి చెందుతుంది — నీలం/వియోలెట్ భాగాన పడుతుంది.

సంక్షిప్తంగా: పరివర్తనం $5\to2$ నుండి విడుదలయ్యే తరంగదైర్ఘ్యం ≈ 434.2 nm, ఇది Balmer శ్రేణి, వర్ణపటంలో దృశ్య (నీల/వయోలెట్) ప్రాంతంలో ఉంటుంది.

ప్రశ్న 18.కక్ష్య (ఆర్బిట్)కు, ఆర్బిటాల్కు గల భేదాన్ని వివరించండి.

జవాబు:

కక్ష్య	ఆర్బిటాల్
1. కేంద్రకం చుట్టూ ఎలక్ట్రాన్ తిరిగే వృత్తాకార మార్గాన్ని కక్ష్య అంటారు.	1. ఎలక్ట్రాన్ కనుగొనే అధిక సంభావ్యత గల త్రిమితీయ ప్రాంతాన్ని ఆర్బిటాల్ అంటారు.
2. ఇవి దిశారహితమైనవి.	2. వీటికి నిర్దిష్ట ఆకృతి ఉండి దిశ ఉంటుంది. (s – ఆర్బిటాల్ తప్ప)
3. ఒక నిర్దిష్ట ‘n’ విలువ (కక్ష్య)లో గరిష్ట ఎలక్ట్రాన్ల సంఖ్య 2n².	3. ప్రతి ఆర్బిటాల్ గరిష్టంగా రెండు ఎలక్ట్రాన్లను మాత్రమే ఉంచగలదు.

ప్రశ్న 19.కాంతి విద్యుత్ ప్రభావాన్ని వివరించండి.

జవాబు:కాంతి ఒక తరంగం మాత్రమే కాదు, అది సూక్ష్మ కణాల సమూహం (ఫోటాన్లు) గా కూడా ప్రవర్తిస్తుంది అని ఐన్‌స్టీన్ తన క్వాంటం సిద్ధాంతం ద్వారా వివరించాడు. ప్రతి ఫోటాన్‌ శక్తి, దాని పౌనఃపున్యానికి (ν) అనురూపంగా ఉంటుంది.

దానిని ఈ సమీకరణంతో వ్యక్తం చేస్తారు:

$$E = h\nu$$

ఇక్కడ

• $h$ = ప్లాంక్ స్థిరాంకం

• $\nu$ = కాంతి యొక్క పౌనఃపున్యం

లోహం ఉపరితలంపై ఫోటాన్ ఢీకొన్నప్పుడు, దాని శక్తిని లోహంలోని ఎలక్ట్రాన్ గ్రహిస్తుంది. ఫోటాన్ శక్తి, ఆ లోహం నుంచి ఎలక్ట్రాన్ బయటకు రావడానికి కావలసిన వర్క్ ఫంక్షన్ (W) కంటే ఎక్కువగా ఉంటే, ఎలక్ట్రాన్ విడుదల అవుతుంది.

మిగిలిన శక్తి విడుదలైన ఎలక్ట్రాన్ గతిజశక్తిగా మారుతుంది:

$$h\nu = W + KE$$ $$h\nu = h\nu_{0} + \tfrac{1}{2}mv^{2}$$

ఇక్కడ

• $W = h\nu_{0}$ = వర్క్ ఫంక్షన్ (లోహపు ఆకర్షణ బలాన్ని అధిగమించడానికి కావలసిన కనీస శక్తి)

• $KE$ = విడుదలైన ఎలక్ట్రాన్ గతిజశక్తి

• $m$ = ఎలక్ట్రాన్ ద్రవ్యరాశి

• $v$ = ఎలక్ట్రాన్ వేగం

ఉదాహరణకు, ఎరుపు కాంతి ఫోటాన్ శక్తి తక్కువగా ఉండటంతో కొన్ని లోహాలనుంచి ఎలక్ట్రాన్ విడుదల చేయలేను. కానీ, ఊదా కాంతి ఫోటాన్‌ శక్తి ఎక్కువగా ఉండటం వలన, ఆ లోహం నుంచి ఎలక్ట్రాన్లు సులభంగా బయటకు వస్తాయి.

👉 ఈ విధంగా, కాంతి విద్యుత్ ప్రభావాన్ని సరైన రీతిలో ఐన్‌స్టీన్ వివరించాడు.

దీర్ఘ సమాధాన ప్రశ్నలు

ప్రశ్న 1.రూథర్ ఫర్డ్ పరమాణువు కేంద్రక నమూనాను వివరించండి. దానిలోని లోపాలు ఏమిటి?

జవాబు:బంగారు రేకుల ప్రయోగం (Gold Foil Experiment):

రూథర్‌ఫోర్డ్ తన విద్యార్థులు గైగర్, మార్స్‌డెన్‌లతో కలిసి α–కణాలను పలుచని బంగారు రేకులపై ప్రసరింపజేశాడు. పరిశీలనలో ఆయన కింది ఫలితాలను గమనించాడు:

1. ఎక్కువ భాగం α–కణాలు ఎలాంటి వ్యత్యాసం లేకుండా రేకుల గుండా నేరుగా వెళ్లిపోయాయి.

2. కొద్దిపాటి α–కణాలు చిన్న కోణాల్లో వ్యత్యాసం చెంది దిశ మార్చుకున్నాయి.

3. చాలా అరుదైన α–కణాలు సుమారు 180° కోణంలో తిరిగి వచ్చాయి.

నిష్కర్షలు (Conclusions):
ఈ పరిశీలనల ఆధారంగా రూథర్‌ఫోర్డ్ తన కేంద్రక నమూనాను ప్రతిపాదించాడు.

1. పరమాణువు ఎక్కువ భాగం ఖాళీ స్థలంతో నిండి ఉంటుంది.

2. పరమాణువు మొత్తం ధనవిద్యుత్‌భారం (positive charge) పరమాణువు మధ్యలోని చిన్న భాగంలో కేంద్రీకృతమై ఉంటుంది. దీన్నే కేంద్రకం (Nucleus) అంటారు.

3. కేంద్రకం చుట్టూ ఎలక్ట్రాన్లు అధిక వేగంతో గుండ్రటి మార్గాల్లో తిరుగుతాయి. వీటినే కక్ష్యలు (Orbits) అంటారు.

4. కేంద్రకం మరియు ఎలక్ట్రాన్లు స్థిర విద్యుదాకర్షణ శక్తి వల్ల బలంగా అనుసంధానమై ఉంటాయి.

5. ఈ నమూనా, సౌరవ్యవస్థను పోలి ఉండటం వల్ల దీనిని సౌరవ్యవస్థ నమూనా (Solar System Model) అంటారు.

---

రూథర్‌ఫోర్డ్ నమూనా లోపాలు:

1. పరమాణు స్థిరత్వ సమస్య:
   విద్యుదయస్కాంత సిద్దాంతం ప్రకారం, వృత్తాకార మార్గంలో తిరిగే ఛార్జ్ ఉన్న కణం నిరంతరం వికిరణం (radiation) విడుదల చేస్తుంది. ఫలితంగా శక్తి కోల్పోయి చివరికి ఎలక్ట్రాన్ కేంద్రకంలో పడిపోవాలి. కానీ వాస్తవంలో పరమాణువులు స్థిరంగా ఉంటాయి. దీనికి ఈ నమూనా సమాధానం ఇవ్వలేదు.

2. ఎలక్ట్రాన్ నిర్మాణం తెలియకపోవడం:
   ఎలక్ట్రాన్లు కేంద్రకం చుట్టూ ఎలా ఏర్పాటు అయ్యాయో, వాటి శక్తి స్థాయిలు ఎలా ఉన్నాయో ఈ నమూనా వివరించలేదు.

3. వర్ణపట సమస్య:
   హైడ్రోజన్ పరమాణువు వంటివాటిలో కనిపించే గీతల వర్ణపటాలను ఈ నమూనా వివరిస్తే సాధ్యపడలేదు.

---

👉 కాబట్టి, రూథర్‌ఫోర్డ్ నమూనా పరమాణువులో కేంద్రక ఉనికిని నిరూపించినా, పరమాణు స్థిరత్వం మరియు ఎలక్ట్రాన్ పంపిణీని వివరించడంలో విఫలమైంది.

ప్రశ్న 2.ప్లాంక్స్ క్వాంటమ్ సిద్ధాంతాన్ని సంక్షిప్తంగా వివరించండి.

జవాబు:ప్లాంక్ ప్రతిపాదనలు :

1. ఎలక్ట్రాన్ లాంటి ఆవేశభరిత కణాలు కంపించేటప్పుడు శక్తి విడుదల అవుతుంది.

2. ఈ శక్తి నిరంతరంగా కాకుండా సూక్ష్మ ప్యాకెట్లు (quanta) రూపంలో ఉద్గారమవుతుంది.

3. ఒక్కో ప్యాకెట్‌ను క్వాంటం అంటారు. కాంతి సందర్భంలో దానిని ఫోటాన్ అంటారు.

4. ప్రతి క్వాంటం యొక్క శక్తి సూత్రం :

   $$E = hν \quad (లేదా) \quad E = nhν$$

   • ఇక్కడ h = ప్లాంక్ స్థిరాంకం (6.625 × 10⁻²⁷ ఎర్గ్–సెకన్ లేదా 6.625 × 10⁻³⁴ జౌల్–సెకన్)

   • ν = ఆవర్తనం (frequency)

   • n = పూర్ణాంకం

5. శక్తి క్వాంటీకరణం (quantisation) జరుగుతుంది. అంటే శక్తి శోషణం లేదా ఉద్గారం ఒక క్వాంటం లేదా దాని పూర్ణ గుణితాల రూపంలోనే జరుగుతుంది.

ప్లాంక్ స్థిరాంకం విలువలు :

• 6.625 × 10⁻²⁷ ఎర్గ్ – సెకన్

• 6.625 × 10⁻³⁴ జౌల్ – సెకన్

• 1.58 × 10⁻³⁴ కాలరీ – సెకన్

సిద్ధాంతం విజయము :

• కృష్ణ పదార్థ వికిరణాల (Black body radiation) వివరణలో ఈ సిద్ధాంతం అత్యంత విజయవంతంగా నిలిచింది.

• కృష్ణ పదార్థం అనగా శక్తిని పూర్తిగా శోషించగలిగే లేదా పూర్తిగా ఉద్గరించగలిగే పదార్థం.

ప్రశ్న 3.హైడ్రోజన్ పరమాణువు బోర్ నమూనా ప్రతిపాదనలు ఏమిటి? [A.P. Mar. 15 Mar. 13]

జవాబు:బోర్ ప్రతిపాదనలు (Bohr’s Postulates):

1. స్థిర కక్ష్యలు (Stationary orbits):
   హైడ్రోజన్ పరమాణువులో ఎలక్ట్రాన్ కేంద్రకం చుట్టూ నిర్దిష్ట వ్యాసార్థాల వృత్తాకార మార్గాల్లో మాత్రమే తిరుగుతుంది. వీటిని స్థిర స్థితులు లేదా శక్తి స్థాయిలు అంటారు.

2. శక్తి స్థిరత్వం (Energy constancy):
   ఎలక్ట్రాన్ ఒక కక్ష్యలో తిరుగుతున్నప్పుడు దాని శక్తి మారదు.

3. శక్తి మార్పులు (Energy changes):
   ఎలక్ట్రాన్ ఒక కక్ష్య నుండి మరొక కక్ష్యకు మారినప్పుడు మాత్రమే శక్తి మార్పు జరుగుతుంది.

   • తక్కువ శక్తి స్థాయి → ఎక్కువ శక్తి స్థాయి కు వెళితే శక్తి శోషణ జరుగుతుంది.

   • ఎక్కువ శక్తి స్థాయి → తక్కువ శక్తి స్థాయి కు వస్తే శక్తి ఉద్గారం జరుగుతుంది.

   ఈ శక్తి వ్యత్యాసం :

   $$ΔE = E_2 - E_1 = hν$$

4. కోణీయ భ్రమణ గతి (Quantisation of angular momentum):
   ఎలక్ట్రాన్ యొక్క కోణీయ భ్రమణ గతి

   $$mvr = \frac{nh}{2π}$$

   రూపంలో ఉండాలి. (n = 1, 2, 3 …)

---

హైడ్రోజన్ వర్ణపటానికి వివరణ (Hydrogen spectrum):

• రెండు స్థిర స్థితుల మధ్య ఎలక్ట్రాన్ పరివర్తన వల్ల కాంతి కిరణం ఉద్గారమవుతుంది లేదా శోషించబడుతుంది.

• శోషణ వర్ణపటం (Absorption spectrum): ఎలక్ట్రాన్ తక్కువ స్థాయి నుండి ఎక్కువ స్థాయికి వెళ్తే (n_f > n_i).

• ఉద్గార వర్ణపటం (Emission spectrum): ఎలక్ట్రాన్ ఎక్కువ స్థాయి నుండి తక్కువ స్థాయికి వస్తే (n_i > n_f).

• ప్రతి వర్ణరేఖ ఒక ప్రత్యేక పరివర్తన ఫలితం.

• పెద్ద సంఖ్యలో హైడ్రోజన్ పరమాణువులు ఉంటే అనేక వర్ణపట రేఖలు కనబడతాయి.

ప్రశ్న 4.హైడ్రోజన్ పరమాణువుకు బోర్ సిద్ధాంత విజయాలను వివరించండి.
జవాబు:

1. ప్రధాన క్వాంటం సంఖ్య (n) పరిచయం:
   బోర్ सिद्धాంతం ఎలక్ట్రాన్ నిర్దిష్ట స్థిర కక్ష్యల్లో (n = 1, 2, 3, …) మాత్రమే తిరగగలదని చూపించింది. ప్రతి n విలువ ఒక ప్రధాన క్వాంటం సంఖ్యగా భావించబడింది.

2. కక్ష్యల పరిమాణం మరియు వ్యాసార్థం:
   ఎలక్ట్రాన్ కక్ష్యల వ్యాసార్థం n² కు అనుగుణంగా ఉంటుంది. ఉదాహరణకు:

   $$r_n = 0.529 \times n^2 \text{ Å} = 52.9 \times n^2 \text{ pm}$$

3. ఎలక్ట్రాన్ శక్తి స్థాయిలు (Energy Levels):
   ఎలక్ట్రాన్ శక్తి స్థాయిలు క్వాంట్ నంబర్ ఆధారంగా నిర్ణయించబడతాయి:

   $$E_n = -R_H \frac{1}{n^2}, \quad n = 1, 2, 3, \dots$$

   ఇక్కడ $R_H$ = 1,09,677 cm⁻¹ (రిడ్బర్గ్ స్థిరాంకం).

4. హైడ్రోజన్ యొక్క రేఖా వర్ణపటాన్ని వివరించడం:
   బోర్ సిద్ధాంతం హైడ్రోజన్ అటామ్లోని ఎలక్ట్రాన్‌లు ఒక కక్ష్య నుండి మరొక కక్ష్యకు మారినప్పుడు వస్తున్న కాంతి రేఖలను వివరించింది.

5. హైడ్రోజన్‌ వంటి అయాన్లకు వర్తింపు:
   He⁺, Li²⁺, Be³⁺ వంటి ఏక ఎలక్ట్రాన్ అయాన్లకు కూడా ఈ సిద్ధాంతం అన్వయించబడుతుంది.

6. ఎలక్ట్రాన్ వేగం గురించి వివరణ:
   ఎలక్ట్రాన్ ఒక స్థిర కక్ష్యంలో తిరిగే వేగం ఖచ్చితంగా నిర్వచించబడింది, దీని వల్ల ఎలక్ట్రాన్‌లు శక్తిని నిరంతరంగా విడుదల చేయకుండా ఉంటాయి.

అంటే, బోర్ సిద్ధాంతం హైడ్రోజన్ అటాం యొక్క కవర్ నిర్మాణం, కక్ష్య పరిమాణం, శక్తి స్థాయిలు, వర్ణపటాలు, మరియు ఎలక్ట్రాన్ స్థిరత్వం వంటి అంశాలను విజయవంతంగా వివరించింది.

తక్కువగా, ఎలక్ట్రాన్ స్థిర కక్ష్యల్లో మాత్రమే ఉండగలగడం, క్షేత్రరేఖ వర్ణపటం వివరణ, మరియు వేర్వేరు అయాన్లకు అన్వయం – ఇవే బోర్ సిద్ధాంత ప్రధాన విజయాలు.

ప్రశ్న 5.
పరమాణువు క్వాంటమ్ యాంత్రిక నమూనా సిద్ధాంతానికి దారితీసిన కారణాలను వివరించండి.
జవాబు:

1. సంప్రదాయ యాంత్రిక శాస్త్ర పరిమితులు:

• కLASిక్ యాంత్రిక శాస్త్రం పెద్ద వస్తువుల (రాయులు పడడం, గ్రహాల చలనం) కోసం చక్కగా పని చేసింది.

• కానీ, ఎలక్ట్రాన్, పరమాణు వంటి సూక్ష్మ కణాల చలనాన్ని ఇది వివరించలేకపోయింది.

• పదార్థాల **ద్వంద్వ స్వభావం (Wave-Particle Duality)**ను కూడా క్లాసిక్ యాంత్రిక శాస్త్రం వివరించలేకపోయింది.

---

2. క్వాంటమ్ యాంత్రిక శాస్త్రం నిర్వచనం:

• క్వాంటమ్ యాంత్రిక శాస్త్రం అంటే:
  సూక్ష్మ కణాల చలనాన్ని, వాటి ద్వంద్వ స్వభావాన్ని పరిగణనలోకి తీసుకొని వివరించే శాస్త్రం.

• ఇది ఎలక్ట్రాన్ వంటి సూక్ష్మ కణాల ప్రవర్తన, శక్తి స్థాయిలను వివరించగలదు.

---

3. పరమాణు క్వాంటమ్ యాంత్రిక నమూనా ముఖ్య లక్షణాలు:

1. ఎలక్ట్రాన్ శక్తి స్థాయిలు క్వాంటీకృతం అవుతాయి:
   ఎలక్ట్రాన్ స్థిరమైన క్వాంటం శక్తి స్థాయిలలో మాత్రమే ఉండగలదు.

2. క్వాంటీకృత శక్తి స్థాయిల కారణం:

   • ఎలక్ట్రాన్ కి తరంగదైర్ఘ్యాలు ఉన్నాయి.

   • ప్రోడింగల్ తరహా సమీకరణానికి ఆమోదయోగ్యమైన విలువలు మాత్రమే సాధ్యం అవుతాయి.

3. ఎలక్ట్రాన్ సమాచారం ఆర్బిటాల్ తరంగ ప్రమేయంలో ఉంటుంది:

   • ఎలక్ట్రాన్ యొక్క సమాచారం, ‘Ψ’ అనే ఆర్బిటల్ తరంగ ప్రమేయం ద్వారా ప్రతిబింబిస్తుంది.

   • క్వాంటమ్ యాంత్రిక శాస్త్రం ద్వారా ఈ సమాచారాన్ని బయటకు తీయవచ్చు.

4. ఎలక్ట్రాన్ మార్గం కచ్చితంగా తెలియదు:

   • ఎలక్ట్రాన్ ఎక్కడ ఉంటుందో సంభావ్యత రూపంలో మాత్రమే చెప్పవచ్చు.

   • ఒక బిందువులో ఎలక్ట్రాన్ ఉండే సంభావ్యత = $(Ψ)^2$ → దీనిని సంభావ్యతా సాంద్రత అంటారు.

   • $(Ψ)^2$ ఎప్పుడూ ధన విలువ అవుతుంది.

5. కేంద్రం చుట్టూ ఎలక్ట్రాన్ ఎక్కువగా ఉండే ప్రదేశం:

   • వేర్వేరు బిందువుల $(Ψ)^2$ విలువలు తెలుసుకుంటే, ఎలక్ట్రాన్ ఉండే అధిక సంభావ్యత గల ప్రదేశంని గుర్తించవచ్చు.

---

సంక్షేపంగా:
క్వాంటమ్ యాంత్రిక నమూనా సూక్ష్మ కణాల స్వభావాన్ని, శక్తి స్థాయిలను, మరియు ఎలక్ట్రాన్ సంభావ్యతను విజయవంతంగా వివరించగలదు.

• 
  

ప్రశ్న 6.పరమాణు క్వాంటమ్ యాంత్రిక నమూనా ముఖ్య లక్షణాలను వివరించండి.
జవాబు:

1. ఎలక్ట్రాన్ శక్తి క్వాంటీకరణ

• పరమాణువులోని ఎలక్ట్రాన్ శక్తి నిర్దిష్ట, క్వాంటీకృత స్థాయిలలో మాత్రమే ఉంటుంది.

• ఇది ఎలక్ట్రాన్‌ను నిరంతర శక్తి మార్పుల నుండి రక్షిస్తుంది.

2. క్వాంటీకృత స్థాయిల కారణం

• ఎలక్ట్రాన్‌కు తరంగదైర్ఘ్యాలు ఉండటం.

• ప్రోడింగల్ తరహా సమీకరణానికి అనుగుణమైన విలువలు మాత్రమే సాధ్యం అవుతాయి.

• వీటివల్లే ఎలక్ట్రాన్ శక్తి స్థాయిలు నిర్దిష్టంగా ఉంటాయి.

3. ఆర్బిటల్ తరంగ ప్రమేయం (Ψ)

• ఎలక్ట్రాన్ గురించి మొత్తం సమాచారం ఆర్బిటల్ తరంగ ప్రమేయం Ψలో ఉంటుంది.

• క్వాంటమ్ యాంత్రిక శాస్త్రం ద్వారా ఈ సమాచారాన్ని విశ్లేషించవచ్చు.

4. ఎలక్ట్రాన్ మార్గం స్పష్టంగా తెలియదు

• ఎలక్ట్రాన్ ఒక ఖచ్చితమైన మార్గంలో తిరిగేలా చెప్పలేం.

• కాబట్టి, ఎలక్ట్రాన్ సంభావ్యత రూపంలో మాత్రమే వివరించబడుతుంది.

5. సంభావ్యతా సాంద్రత (Ψ²)

• ఒక నిర్దిష్ట బిందువు వద్ద ఎలక్ట్రాన్ ఉండే సంభావ్యత = (Ψ)².

• Ψ² ఎప్పుడూ ధన విలువ.

• వేర్వేరు బిందువుల Ψ² విలువలు తెలుసుకుంటే, ఎలక్ట్రాన్ ఎక్కువగా ఉండే ప్రదేశాన్ని గుర్తించవచ్చు.

---

సంక్షేపంగా:

• ఎలక్ట్రాన్ శక్తి క్వాంటీకృతం,

• ఆర్బిటల్ లో సమాచారం Ψ లో,

• మార్గం ఖచ్చితంగా తెలియకపోవడం,

• సంభావ్యతా సాంద్రత (Ψ²) ద్వారా ఎలక్ట్రాన్ ఎక్కువగా ఉండే ప్రదేశం గుర్తించబడటం — ఇవే పరమాణు క్వాంటమ్ యాంత్రిక నమూనా ప్రధాన లక్షణాలు.

ప్రశ్న 7.బోర్ పరమాణు నమూనాలోని లోపాలు ఏమిటి? [A.P. Mar. ’15 Mar. ’13]
జవాబు:

బోర్ నమూనా లోపాలు:

1. బహుళ ఎలక్ట్రాన్ పరమాణువులు:

   • ఒకటి కంటే ఎక్కువ ఎలక్ట్రాన్లు ఉన్న పరమాణువులు లేదా అయాన్ల వర్ణపటాన్ని బోర్ నమూనా వివరించలేదు.

2. సూక్ష్మ వర్ణపటం (Fine Structure):

   • హైడ్రోజన్ వర్ణపటంలోని గీతలు అంతర్గతంగా విభజింపబడే సూక్ష్మ గీతలను (fine lines) బోర్ నమూనా వివరించలేదు.

3. జీమన్ మరియు స్టార్క్ ప్రభావాలు:

   • జీమన్ ఫలితం: బాహ్య అయస్కాంత క్షేత్రంలో వర్ణపటంలోని గీతలు సున్నిత గీతలుగా చీలడం.

   • స్టార్క్ ప్రభావం: విద్యుత్ క్షేత్రంలో వర్ణపటంలోని గీతలు సున్నిత గీతలుగా విభజించడం.

   • బోర్ నమూనా వీటిని వివరించలేకపోయింది.

4. ఎలక్ట్రాన్ ద్వంద్వ స్వభావం:

   • ఎలక్ట్రాన్ ఫోటాన్ లాగా కూడా ప్రవర్తిస్తుందని, ద్వంద్వ స్వభావాన్ని బోర్ నమూనా వివరించలేదు.

5. కోణీయ ద్రవ్యవేగం నియమం:

   • ఎలక్ట్రాన్ కోణీయ ద్రవ్యవేగం $L = n \frac{h}{2\pi}$ అనేది పూర్తిస్థాయిలతో గుణితంగా ఉండాలి అని ప్రతిపాదించాడు, కానీ దీని వెనుక కారణాన్ని వివరించలేదు.

6. త్రిమితీయ కక్ష్య స్థానం:

   • బోర్ నమూనా ఎలక్ట్రాన్ కక్ష్యలు సమతలంలోనే ఉంటాయని సూచిస్తుంది, ఇది తప్పు.

7. రసాయన బంధాల సామర్థ్యం:

   • బోర్ నమూనా పరమాణువులు రసాయన బంధాల ద్వారా అణువులను ఏర్పరిచే సామర్థ్యాన్ని వివరించలేకపోయింది.

---

సంక్షేపంగా:

• బహుళ ఎలక్ట్రాన్ల వర్ణపటం, సూక్ష్మ వర్ణపటం, జీమన్-స్టార్క్ ప్రభావాలు, ఎలక్ట్రాన్ ద్వంద్వ స్వభావం, కోణీయ ద్రవ్యవేగం వెనుక కారణం, త్రిమితీయ కక్ష్యల అమరిక, రసాయన బంధ సామర్థ్యం – ఇవన్నీ బోర్ నమూనా పరిధిలో లేవు.

---

ఇచ్చిన వివరాలతో, బోర్ నమూనా పరిమితులను స్పష్టంగా అర్థం చేసుకోవచ్చు.

ప్రశ్న 8.ఎలక్ట్రాన్ ద్వంద్వ స్వభావానికి రుజువులు ఏమిటి?
జవాబు:

1. కాంతి ఉదాహరణలు

• కణ స్వభావం:

  • కాంతి క్వాంటాలు (ఫోటోన్లు) కృష్ణ వస్తువుల నుండి వచ్చే వికిరణాలను మరియు కాంతి విద్యుత్ ప్రభావాన్ని వివరించాయి.

  • దీని ద్వారా కాంతి కణాలుగా ప్రవర్తిస్తుందని గుర్తించవచ్చు.

• తరంగ స్వభావం:

  • కాంతి వివర్తనం (Diffraction), వ్యతికరణం (Interference) వంటి ప్రక్రియలను కూడా చూపిస్తుంది.

  • దీని ద్వారా కాంతి తరంగాలుగా కూడా ప్రవర్తిస్తుంది.

అంటే, కాంతికి ద్వంద్వ స్వభావం ఉంది → తరంగం మరియు కణం రెండూ.

---

2. డీబ్రోలీ సిద్ధాంతం

• ప్రకారం: ఎలక్ట్రాన్ వంటి కణాలకు కూడా ద్వంద్వ స్వభావం ఉంటుంది.

• డీబ్రోలీ సమీకరణం:

  $$\lambda = \frac{h}{p}$$

  • ఇక్కడ $\lambda$ = తరంగదైర్ఘ్యం, $h$ = ప్లాంక్ స్థిరాంకం, $p$ = కణం యొక్క గుణాకార ద్రవ్యవేగం.

• దీని ద్వారా ఎలక్ట్రాన్ తరంగంగా కూడా ప్రవర్తిస్తుంది.

---

3. హైసన్ బర్గ్ అనిశ్చితత్వ నియమం (Heisenberg Uncertainty Principle)

• నియమం:

  • ఎలక్ట్రాన్ వంటి సూక్ష్మ కణం యొక్క స్థానం (∆x) మరియు ద్రవ్యవేగం (∆p) ను ఒకేసారి ఖచ్చితంగా కొలవడం సాధ్యం కాదు.

  $$(∆x)(∆p) \ge \frac{h}{2\pi}$$

• ప్రాముఖ్యత:

  1. ఎలక్ట్రాన్ కు స్థిర కక్ష్యం లేదా ఖచ్చితమైన ప్రక్షేప మార్గం ఉండదు.

  2. ఈ నియమం సూక్ష్మ కణాలకే వర్తిస్తుంది, స్థూల కణాలకు కాదు.

  3. మిల్లీగ్రాము స్థూల కణాలకు అనిశ్చితత్వ ఫలితాలు ఉండవు.

---

సారాంశం:

• కాంతి ద్వారా రెండుసార్లు చూపినది → Wave-Particle Duality.

• డీబ్రోలీ सिद्धాంతం → ఎలక్ట్రాన్ కు కూడా ద్వంద్వ స్వభావం.

• హైసన్ బర్గ్ నియమం → ఎలక్ట్రాన్ స్థానం, ద్రవ్యవేగం ఖచ్చితంగా చెప్పలేము.

• 
  

Answer by  Mrinmoee