সংহতি | Lesson 1 | Exercise 1.2 | Class 10 Advanced Maths Solution Assam | Class 10 Advanced Mathematics Solution Assamese Medium | দশম শ্ৰেণীৰ উচ্চ গণিতৰ প্ৰশ্ন উত্তৰ |

পাঠ ১

সংহতি

Sets

Exercise 1.2

1. যদি A = {1, 3, 5} আৰু B = {2, 4, -1} তেন্তে A x B আৰু B x A উলিওৱা। A x B আৰু B x A ত কিমান মৌল আছে নিৰ্ণয় কৰা।

উত্তৰঃ 

দিয়া আছে;

A = { 1, 3, 5} আৰু B = { 2, 4, -1}

∴ A x B = {(1, 2), (1, 4) (1, -1), (3, 2), (3, 4), (3, -1), (5, 2), (5, 4), (5, -1)}

B x A = {(2, 1), (2, 3), (2, 5), (4, 1), (4, 3), (4, 5), (-1, 1), (-1, 3), (-1, 5)}

∴ A x B আৰু B x A ত 9 টাকৈ মৌল আছে।

2.

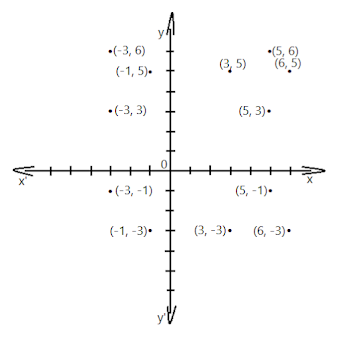
(a) যদি A = {-1, 3, 6} আৰু B = {-3, 5} A x B আৰু B x A উলিওৱা। এই কাৰ্টেজীয় গুণফল দুটাৰ লেখ অংকন কৰা।

উত্তৰঃ 

দিয়া আছে;

A = {-1, 3, 6} আৰু B = {-3, 5}

∴ A x B = {(-1, -3), (-1, 5), (3, -3), (3, 5), (6, -3), (6, 5)}

আৰু B x A = {(-3, -1), (-3, 3), (-3, 6), (5, -1), (5, 3), (5, 6)}

(b) যদি A = {2, 4}, B = {-1, 3, 7}, C = {1, 0}তেনেহ'লে বৃক্ষচিত্ৰৰ সহায়ত A x B, B x A আৰু A x B x C নিৰ্ণয় কৰা।

উত্তৰঃ 

দিয়া আছে;

A = {2, 4} আৰু B = {-1, 3, 7}

∴ A x B = {(2, - 1), (2, 3), (2,7), (4, -1), (4, 3), (4, 7)}

∴ B x A = {(-1, 2), (-1, 4), (3, 2), (3, 4), (7, 2), (7, 4)}

∴ A x B x C = {(2, -1, 1), (2, -1, 0), (2, 3, 1), (2, 3, 0), (2, 7, 1), (2, 7, 0), (4, -1, 1), (4, -1, 0), (4, 3, 1), (4, 3, 0), (4, 7, 1), (4, 7, 0)}

3. যদি A = {x, y, u, v} আৰু B = {a, b, l, m} তেন্তে A x B উলিওৱা আৰু এই কাৰ্টেজীয় গুণফলক এটা স্থানাংক চিত্ৰৰ দ্বাৰা প্ৰতিনিধিত্ব কৰা।

উত্তৰঃ

দিয়া আছে; 

A = {x, y, u, v} আৰু B = {a, b, l, m}

∴ A x B = {(x, a), (x, b), (x, l), (x, m), (y, a), (y, b), (y, l), (y, m), (u, a), (u, b), (u, l), (u, m), (v, a), (v, b), (v, l), (v, m)}

4. যদি A = {3, 5}, B = {1, 2, 4}, C = {3, 4, 6} তেন্তে দেখুওৱা যে 一

(i) A x (B∪C) = (A x B)∪(A x C)

উত্তৰঃ 

LHS; A x (B∪C)

= {3, 5} x {1, 2, 3, 4, 6}

= {(3, 1), (3, 2), (3, 3), (3, 4), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 6)}

আকৌ,

RHS; (A x B)∪(A x C)

= [{3, 5} x {1, 2, 4}]∪[{3, 5} x {3, 4, 6}]

= [{(3, 1), (3, 2), (3, 4), (5, 1), (5, 2), (5, 4)}]∪[{(3, 3), (3, 4), (3, 6), (5, 3), (5, 4), (5, 6)}]

= {(3, 1), (3, 2), (3, 3), (3, 4), (3, 4), (5, 1), (5, 2), (5, 3), (5, 4), (5, 6)}

∴ LHS = RHS

(ii) A x (B∩C) = (A x B)∩(A x C)

উত্তৰঃ

LHS; A x (B∩C)

= {3, 5} x {4}

= {(3, 4), (5, 4)}

আকৌ, 

RHS; (A x B)∩(A x C)

= [{3, 5} x {1, 2, 4}]∩[{3, 5} x {3, 4, 6}]

= [{(3, 1), (3, 2), (3, 4), (5, 1), (5, 2), (5, 4)}]∩[{(3, 3), (3, 4), (3, 6), (5, 3), (5, 4), (5, 6)}]

= {(3, 4), (5, 4)}

∴ LHS = RHS

5. A = {x: x ∊ I আৰু -2 < x < 4} আৰু B = {y: y ∊ I হ'ল y² – 9 = 0 ৰ মূল } সংহতি দুটাৰ বাবে  A x B লেখ অংকন কৰা n(A x B) উলিওৱা।

উত্তৰঃ 

A = {-1, 0, 1, 2, 3} আৰু B = {-3, 3}

∴ A x B = {(-1, -3), (-1, 3), (0, -3), (0, 3), (1, -3), (1, 3), (2, -3), (2, 3), (3, -3), (3, 3)}

আৰু n(A x B) = 10

6. যদি A = {-3, 0, 3} আৰু {-1, 1} তেন্তে দুখন বেলেগ বেলেগ স্থানাংক তলত A x B আৰু B x A লেখ অংকন কৰা।

উত্তৰঃ

A x B = {(-3, -1), (-3, 1), (0, -1), (0, 1), (3, -1), (3, 1)}

আৰু B x A = {(-1, -3), (-1, 0), (-1, 3), (1, -3), (1, 0), (1, 3)}

A x B

B x A

7. (i) যদি A = ф আৰু B = {-1, 1} তেন্তে A x B, B x A আৰু B² ৰ ঘাত সংহতি নিৰ্ণয় কৰা।

উত্তৰঃ 

দিয়া আছে;

A = ф, B = {-1, 1}

এতিয়া, A x B = ф

∴ p(A x B) = {ф}

আৰু B x A = ф

∴ p(B x A) = {ф}

আৰু p(B x B) = {ф}, {(-1, -1)}, {(-1, 1)}, {(1, -1)}, {(1, 1)}, {(-1, -1), (-1, 1)}, {{(-1, -1), (1, -1)}, {(-1, -1), (1, 1)}, {(-1, -1), (-1, 1), (1, -1)}, {(-1, -1), (-1, 1), (1, 1)}, {(-1, 1), (-1, 1), (1, -1), (1, 1)}, B x B}

(ii) যদি A = {0} আৰু B = {1} তেন্তে A x B আৰু B x A নিৰ্ণয় কৰা লগতে p(A x B) আৰু p(B x A) উলিওৱা।

উত্তৰঃ 

A x B = {(0, 1)}

∴ p(A x B) = {ф, A x B}

আৰু B x A = {(1, 0)}

∴ p( B x A) = {ф, B x A}

8. যদি A = {2, 4} আৰু B = {4, 2} তেনেহ'লে আমি A x B = A²   আৰু B x A = B² বুলি লিখিব পাৰিমনে?

উত্তৰঃ 

দিয়া আছে;

A = {2, 4} আৰু B = {4, 2}

∴ A x B = {2, 4} x {4, 2}

= {(2, 4), (2, 2), (4, 4), (4, 2)}

আকৌ, A x A = {2, 4} x {2, 4}

= {(2, 2), (2, 4), (4, 2), (4, 4)}

B x A = {4, 2} x {2, 4}

= {(4, 2), (4, 4), (2, 2), (2, 4)}

আকৌ, B x B = {4, 2} x {4, 2}

= {(4, 4), (4, 2), (2, 4), (2, 2)}

∴ A x B = A x A আৰু B x A = B x B বুলি লিখিব পাৰি।

9. যদি n(A) = 3 আৰু A x A ত থকা দুটা মৌল (a, a) আৰু (b, c) তেন্তে A আৰু A x A সংহতি দুটা নিৰ্ণয় কৰা।

উত্তৰঃ 

দিয়া আছে; n(A) = 3

∴ A = {a, b, c}

এতিয়া A x A = {a, b, c}

= {(a, a), (a, b), (a, c), (b, a), (b, b), (b, c), (c, a), (c, b), (c, c)}

10. যদি A ⊆ B আৰু C ⊆ D তেন্তে দেখুওৱা যে A x C ⊆ B x D।

উত্তৰঃ ধৰা হ'ল (a, b) এটা A x C ৰ স্বতন্ত্ৰ মৌল তেন্তে

(a, b) ∊ A x C

⇒ a ∈ A আৰু b ∈ C

⇒ (a, b) ∈ B x D

∴ A x C ⊆ B x D

প্ৰমাণ কৰা হ'ল।

11. যদি A x B = {(m, 1), (n, 3), (m, 3), (n, 1), (m, 2), (n, 2)} তেন্তে A আৰু B সংহতি দুটা উলিওৱা।

উত্তৰঃ A x B = {(m, 1), (2, 3), (m, 3), (n, 1), (m, 2), (n, 2)}

∴ A = {m, n}, আৰু B = {1, 2, 3}

12. যদি A আৰু B দুটা অৰিক্ত সংহতি আৰু A x B = A x C তেন্তে দেখুওৱা যে B = C।

উত্তৰঃ ধৰা হ'ল

b এটা স্বতন্ত মৌল, তেন্তে

(a, b) ∈ A x B, ∀ a ∈ A

⇒ (a, b) ∈ A x C, ∀ a ∈ A [ ∵ A x B = A x C ]

⇒ b ∈ C

অৰ্থাৎ b ∈ B ⇒ b ∈ C

∴ B ⊂ C....................(i)

এতিয়া ধৰা হ'ল c এটা C ৰ স্বতন্ত্ৰ মৌল, তেন্তে

(a, b) ∈ A x C, ∀ a ∈ A

⇒ (a, c) ∈ A x B, ∀ a ∈ A

⇒ c ∈ B

∴ C ⊂ B....................(ii)

(i) আৰু (ii) ৰ পৰা B = C।

13. A = {1, 2}, B = {1, 3, 2} আৰু C = {4, 2, 1} তেন্তে দেখুওৱা যে A² = B² ∩ C² ।

উত্তৰঃ 

A x A = {1, 2} x {1, 2}

= {(1, 1), (1, 2), (2, 1), (2, 2)}

আৰু B x B = {1, 3, 2} x {1, 3, 2}

= {(1, 1), (1, 3), (1, 2), (3, 1), (3, 3), (3, 2), (2, 1), (2, 3), (2, 2)}

আৰু C x C = {4, 2, 1} x {4, 2, 1}

= {(4, 4), (4, 2), (4, 1), (2, 4), (2, 2), (2, 1), (1, 4), (1, 2), (1, 1)}

∴ B² ∩ C² = {(1, 1), (1, 2), (2, 1), (2, 2)}

= A x A

H.P

14. যদি A = {0, 1} তেন্তে A x A x A উলিওৱা।

উত্তৰঃ A x A x A = {0, 1} x {0, 1} x {0, 1}

= {(0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1)}

- Hiru Moni Bora