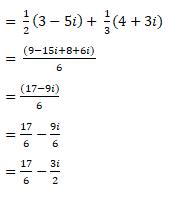পাঠঃ ২
জটিল সংখ্যা
অনুশীলনী 2.1
1. তলত দিয়াবিলাকৰ পৰা কাল্পনিক সংখ্যাবিলাক বাছি উলিওৱা 一
(v) i12
= 1
2. সৰল কৰা 一
(ii) (1 + i)(1 + i)2
= (1 + i)(1 + 2i – 1)
= (1 + i)2i
= 2i – 2
= 2(I – 1)
(iii) (1 + i)(1 + i2)(1 + i3)(1 + i4)
= (1 + i)(1 - 1)(1 – i)(1 + 1)
= (1 + i) x 0 x (1 – i) x 2
= 0
(iv) i38 + i18
= (i2)19 + (i2)9
= (-1)19 + (-1)9
= -1 – 1
= -2
3. তলৰ প্ৰতিটো সংখ্য a + ib আৰ্হিত প্ৰকাশ কৰা
4. তলত দিয়াবিলাকৰ মান নিৰ্ণয় কৰা 一
(b) 1 + i10 + i100 + i1000
= 1 + (i2)5 + (i2)50 – (i2)500
= 1 + (-1)5 + (-1)50 + (-1)500
= 1 – 1 + 1 – 1
= 0
5.
(a) আটাইতকৈ সৰু ধনাত্মক অখণ্ড সংখ্যা n নিৰ্ণয় কৰা যাৰ বাবে (1 + i)2n
= (1 - i)24 সমতাটো সিদ্ধ হয়।
উত্তৰঃ 
(b) যদি n এটা ধনাত্মক অখণ্ড সংখ্যা তেন্তে দেখুওৱা যে
উত্তৰঃ 
6. z1 + z2, z1 – z2 আৰু z1z2 নিৰ্ণয় কৰা, যদিহে z1 আৰু z2 তলত দিয়া ধৰণে হয় 一
(a) z1 = 3 - 4i, z2 = -2 + i
এতিয়া,
z1 + z2
= (3 - 4i) + (- 2 + i)
= 3 - 4i - 2 + i
= 1 - 3i
আৰু
z1 - z2
= (3 - 4i) - (- 2 + i)
= 3 - 4i + 2 - i
= 5 - 5i
আৰু
z1z2
= (3 - 4i)(- 2 + i)
= - 6 + 3i + 8i + 4
= - 2 + 11i
= 11i - 2
(b) z1 = 2 - i, z2 = - 2 - i
এতিয়া;
z1 + z2
= (2 - i) + (- 2 - i)
= 2 - i - 2 - i
= - 2i
আৰু
z1 - z2
= (2 - i) - ( - 2 - i)
= 2 - i + 2 + i
= 4
আৰু
z1z2
= ( 2 - i)(- 2 - i)
= - 4 - 2i + 2i - 1
= - 5
(c) z1 = 1/2(3 - 5i) z2 = 1/3(4 + 3i)
এতিয়া;
(d) z1 = 7 + 3i, z2 = 3i - 7
এতিয়া;
z1 + z2
= ( 7 + 3i) + ( 3i - 7)
= 7 + 3i + 3i - 7
= 6i
z1 - z2
= (7 + 3i) - ( 3i - 7)
= 7 + 3i - 3i + 7
= 14
z1z2
= (7 + 3i)(3i - 7)
= (3i + 7)(3i - 7)
= - 9 - 49
= - 58
(e) z1 = (2 + 3i)(1 - 5i)
= 2 - 10i + 3i + 15
= 17 - 7i
z2 = (1 + i)(3 - i)
3 - i + 3i + 1
4 + 2i
এতিয়া;
z1 + z2
= (17 - 7i) + (4 + 2i)
= 17 - 7i + 4 + 2i
= 21 - 5i
আৰু
z1 - z2
= (17 - 7i) - (4 + 2i)
= 17 - 7i - 4 - 2i
= 13 - 9i
আৰু
z1z2
= (17 - 7i)(4 + 2i)
= 68 + 34i - 28i + 14
= 82 + 6i
7. তলত দিয়া প্ৰতিটো জটিল সংখ্যাকে ক্ৰমিক যোৰৰ যোগফল হিচাপে প্ৰকাশ কৰা
(i) - 3 + 5i
= (- 3, 5)
= -3(1, 0) + 5(0, 1)
(iv) 2
= 2 + i.0
= (2, 0)
= 2(1, 0) + 0(0, 1)
8. যদি x = 3 + 4i আৰু y = 3 - 4i, তেন্তে তলত দিয়াবিলাক নিৰ্ণয় কৰা
9. যদি x = 1 - i তেন্তে দেখুওৱা যে
10. উৎপাদকত প্ৰকাশ কৰা 一
