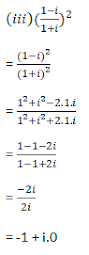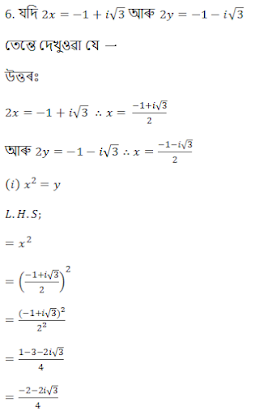জটিল সংখ্যা | Lesson 2 | Exercise 2.2 | Class 10 Advanced Mathematics Solution Assam | Class 10 Advanced Mathematics Solution Assamese Medium | দশম শ্ৰেণীৰ উচ্চ গণিতৰ প্ৰশ্ন উত্তৰ |

পাঠ ২

জটিল সংখ্যা

অনুশীলনী 2.2

1. তলত দিয়া প্ৰতিটো জটিল সংখ্যাৰে সংযুগ্ম আৰু প্ৰতিক্ৰম নিৰ্ণয় কৰা।

(i) - i

ইয়াৰ সংযুগ্ম হৈছে 

i

আৰু প্ৰতিক্ৰম হৈছে

-1/i

= i.i/i

= i

(b) i

ইয়াৰ সংযুগ্ম হৈছে 

- i

আৰু ইয়াৰ প্ৰতিক্ৰম হৈছে 

1/i

= -i.i/i

= -i

(c) 2 + i

ইয়াৰ সংযুগ্ম হৈছে 

2 - i

আৰু প্ৰতিক্ৰম হৈছে 

1/2 + i

= 2- i/(2 + i)(2 - i)

= 2 - i/4 + 1

= 2 - i/5

= 2/5 - i/5

(d) 1/3 + i

= 3 - i/(3 + i)(3 - i)

= 3 - i/ 9 + 1

= 3 - i/10

= 3/10 - i/10

∴ ইয়াৰ সংযুগ্ম হৈছে

3/10 + i/10

ইয়াৰ প্ৰতিক্ৰম হৈছে 

= 3 + i

(e) a + ib

ইয়াৰ সংযুগ্ম হৈছে 

a - ib

আৰু ইয়াৰ প্ৰতিক্ৰম হৈছে 

1/a + ib

= a - ib/(a + ib)(a - ib)

= a - ib/a² + b²

= a/a² + b² - ib/a² + b²

2. a + ib আকাৰত প্ৰকাশ কৰাঃ

(iv) (1 + i)² – (2 + i)²

= 1² + i²  + 2.1.i – (2² + i² + 2.2.i)

= 1 – 1 + 2i – (4 – 1 + 4i)

= 2i – (3 + 4i)

= 2i – 3 – 4i

= - 3 – 2i

(v) (3 + 4i)(12 - 5i)

= 3.12 - 3.5i + 4i.12 - 4i.5i

= 36 - 15i + 48i + 20

= 56 + 33i

3. (a) যদি z₁ = 1 + iআৰু z₂ = 1 - i তেন্তে z_1/z₂ আৰুউলিওৱা।

উত্তৰঃ 

(b) যদি z₁ = 7 + 3i আৰু z₂ = 3i - 7 তেন্তে তলত দিয়াবিলাক নিৰ্ণয় কৰা 一

z₁z₂ 

= ( 7 + 3i)( 3i - 7)

= 21i - 49 - 9 - 21i

= - 58

4. যদি z₁ = 2 + 3i আৰু z₂ = 1 - 2i তেনেহ'লে তলত দিয়াবিলাক সত্যাপন কৰি চোৱা।

উত্তৰঃ 

5. 

(a) যদি z₁ = 2 + i আৰু z₂ = 1 - 3i তেন্তে আৰু নিৰ্ণয় কৰা। সত্যাপন কৰা যে ইহঁত পৰস্পৰ সংযুগ্ম।

উত্তৰঃ 

(b) যিকোনো দুটা জটিল সংখ্যা z₁ আৰু z₂ ৰ বাবে  আৰু এটা আনটোৰ সংযুগ্ম হয়নে নহয় পৰীক্ষা কৰা।

উত্তৰঃ 

7. তলৰ সমীকৰণবোৰ সমাধা কৰা 一

(i) (3x + 5i) – 4y = 10 + (x – 3y)i

⇒ 3x + 5i – 4y = 10 + xi – 3iy  

⇒ 3x + 5i – 4y – 10 – xi + 3yi = 0

⇒ (3x – 4y – 10) + i(-x + 3y + 5) = 0 + i.0

3x – 4y – 10 = 0一 (i)

- x + 3y + 5 = 0一 (ii)

⇒ x = 3y + 5   一 (iii)

(i) ত x ৰ মান বহুৱাই

3(3y + 5) – 4y – 10 = 0

⇒ 9y + 15 – 4y = 10

⇒ 5y = -5

⇒ y = -5/5 = -1

আৰু x = 3y + 5

⇒ x = 3.(-1)+5

⇒ x = -3 + 5

⇒ x = 2

8. যদি তেন্তে দেখুওৱা।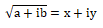

উত্তৰঃ 

 

9. যদি 2a + ib ৰ সংযুগ্ম জটিল (a + 4) - i(a + 2b) তেন্তে a আৰু b ৰ মান উলিওৱা।

উত্তৰঃ 

প্ৰশ্নমতে, 2a - ib = (a + 4) - i(a + 2b)

⇒2a = a + 4    আৰু    b = a + 2b

⇒ 2a - a = 4

⇒ a = 4

আৰু b = a + 2b

⇒b - 2b = a

⇒ -b = 4

⇒b = -4

10. তলৰ জটিল সংখ্যাবিলাকৰ যোগাত্মক আৰু গুণাত্মক বিপৰীত নিৰ্ণয় কৰা।

(i) -4 + i 

ইয়াৰ যোগাত্মক বিপৰীত হৈছে -4 - i

আৰু ইয়াৰ গুণাত্মক বিপৰীত হৈছে 

(ii) (2 + i)(3 - 2i)

= 6 - 4i + 3i +2

= 8 - i

ইয়াৰ যোগাত্মক বিপৰীত হৈছে 

8 + i

আৰু গুণাত্মক বিপৰীত হৈছে 

11. যদি z₁ আৰু z₁ যিকোনো দুটা জটিল সংখ্যা তেন্তে আমি লিখিব পাৰো নে যে

(a) Re(z₁z₂) = Re(z₁)Re(z₂) – Im(z₁)Im(z₂)

(b) Im(z₁z₂) = Re(z₁)Im(z₂) + Im(z₁)Re(z₂)

ধৰো, z₁ = a + ib আৰু z₂ = c + id

∴ z₁z₂

= (a + ib)(c + id)

=ac + aid + bic – bd

= (ac – bd) + i(ad + bc)

(a) Re(z₁z₂) = Re(z₁)Re(z₂) – Im(z₁)Im(z₂)

উত্তৰঃ 

L.H.S;

= Re(z₁z₂)

= ac – bd

R.H.S;

= Re(z₁)Re(z₂) – Im(z₁)Im(z₂)

= ac – bd

∴ L.H.S = R.H.S

(b) Im(z₁z₂) = Re(z₁)Im(z₂) + Im(z₁)Re(z₂)

উত্তৰঃ

L.H.S;

Im(z₁z₂)

= ad + bc

R.H.S;

= Re(z₁)Im(z₂) + Im(z₁)Re(z₂)

= ad + bc

∴ L.H.S = R.H.S

12. 

(i) যদি p + iq = (∝ + i)/(∝ - i) তেন্তে দেখুওৱা যে ∝q = 1 + p

উত্তৰঃ 

p + iq = (∝ + i)/(∝ - i)

⇒ (p + iq)(∝ - i) = ∝ + i

⇒ ∝p - ip + ∝iq +q - ∝ - i

⇒ (∝p + q - ∝) + i(∝q - p - 1) = 0 + i.0 

⇒ ∝p + q - ∝ = 0 

আৰু ∝q - p - 1 = 0

⇒ ∝q = 1 + p

H.P

(ii) যদি x + iy = (a + ib)² তেন্তে x² + y² ৰ মান উলিওৱা।

উত্তৰঃ x + iy = (a + ib)² 

⇒ x + iy = a² - b² + 2.a.ib

⇒ x + iy = ( a² - b² ) + i2ab

⇒ x = a² - b² আৰু y = 2ab

∴ x² + y² 

= ( a² - b²)² + ( 2ab)² 

= a⁴ + b⁴ - 2a²b² + 4a²b² 

= a⁴ + b⁴ + 2a²b²

= ( a² + b²)²

- Hiru Moni Bora